elementaar

Einige Notizen zur Lektüre von Jörg Bewersdorff: "Glück, Logik und Bluff" Ich habe das Buch in der aktuellen, der 7. Auflage gelesen, und was sofort sehr angenehm auffällt ist, daß in den Vorworten zu früheren Auflagen die zahl- und hilfreichen Fehlerverbesserer namentlich genannt werden (darunter auch Pierre Basieux). Das ist zwar gute wissenschaftliche Tradition, es freut einen aber doch, wenn es in dieser Form gemacht wird, und nicht in Fußnoten quasi versteckt. Bewersdorff ordnet die betrachteten Spiele in drei Kategorien: Glücksspiele Kombinatorische Spiele Strategische Spiele Umfänglich macht die Abteilung über reines Glücksspiel lediglich ein knappes Viertel des Buches aus. Das ist zwar nicht so wortkarg wie anderswo, aber auch nicht besonders ausführlich. Für mich war das eher Wiederholungs- und Auffrischungslesen in auffällig angenehmem Erzählton. Die anderen Teile hingegen erwiesen sich als Füllhorn des Vergnügens und der Wissensvermehrung. Da findet sich z.B. eine Tabelle gewichteter Wahrscheinlichkeiten der 40 Felder beim Monopoly-Spiel (verschiedener Jahrgänge und Länderausgaben!), Überlegungen zum Programmieren der ersten Schachcomputer (mit code-Beispielen), Strategiemethoden beim Memory-Spiel, Berechnungen zum Spiel "Mastermind", die beweisen, daß man es als Jugendlicher gewiss nicht immer optimal gespielt hat. Dabei wird natürlich (es ist ein Buch über mathematische Methoden) ab und zu gerechnet, es gibt auch hier und da Formeln. In beider Verwendung zeigt sich allerdings eines der herausragenden Verdienste von Bewersdorff: es wird nicht jede Formel bewiesen, es wird nicht jede Berechnung Schritt für Schritt durchgeführt, statt dessen wird auf mindestens eine Quelle verwiesen, wo man Beweis oder Rechnung ausführlich dargestellt findet. Durch die überaus geschickte Mischung zwischen Ausführlichkeit und einfachem Voraussetzen entsteht so nicht nur dieser angenehme Erzählton, sondern auch andauernde Beweglichkeit im Gehirn. An mindestens drei Stellen musste ich verblüfft inne halten, und das Gelesene, mit "wie kommt er denn jetzt darauf?", mir selbst herleiten. Dies wird noch verstärkt, weil die geschilderten Methoden zwischen "sehr einfach" und "anspruchsvoll" kaum vorhersehbar gemischt sind. Besonders hervorheben möchte ich: den schon erwähnten, durchgehend entspannten Erzählton (beileibe keine Selbstverständlichkeit in dieserart Büchern) und wirklich überragend die phantastische Liste an weiterführender Literatur, in (im Lesefluss tatsächlich lesbaren) Fußnoten und am Ende mancher Kapitel. Das findet man sehr selten und unterstreicht, mit welcher Zugewandtheit der Autor sich seinem Thema widmet. Und diese Zugewandtheit zeigt sich auch im weiteren. Geht es um Wahrscheinlichkeiten erwartet man natürlich das Auftauchen von Pascal, der verschiedenen Bernoullis, Laplace und Poisson, Bayes, Markov und Kolmogorow. Umso schöner aber, daß auch Chevalier de Méré, John Arbuthnot, Emanuel Lasker, (der nicht nur Schachspieler war) und Emile Borel mit ihren Beiträgen gewürdigt werden. Daß mehrmals Edgar Allan Poe zitiert wird, ist genauso ungewöhnlich wie erfreulich und macht eine schätzenswerte Weltoffenheit deutlich. Und z.B. der Fall des Pierre Rémond de Montmort zeigt nicht nur, daß auch in der Neuzeit weiterführende Einsichten sich manchmal bloß durch glücklichen Zufall erhalten haben, wo sich die zeitgenössischen Experten ganz uninteressiert zeigten, sondern auch, wie der Autor ohne Aufhebens die Leistung von Laien, so sie denn erkennbar ist, anerkennt und dem Vergessen entreißt. Das ist so ausgesprochen kenntnisreich wie redlich, verdienstvoll und sympathisch. Zwei Kleinigkeiten sind mir allerdings aufgefallen, wo auch Bewersdorff dem Jargon und der Denkweise von Mathematikern erliegt. An mehreren Stellen schreibt auch er (im Kontext durchaus begründbar) von "der" Normalverteilung, wo es deren doch viele gibt. Auch er kann den Punkt nicht ganz vermeiden, wo bei der Schilderung der Methodik das verwendete Beispiel ins vollständig Irreale kippt, wie in etlichen der angenommenen Pokersituationen. Entfernt sich das Modell zu stark und in entscheidenden Punkten zu sehr von der im Spiel vorgefundenen Wirklichkeit, dann ist das Modell für diese Wirklichkeit eben nicht geeignet. Die Gefahr ist dann groß, daß der eventuelle Lernfortschritt in der Methodik mehr als zugedeckt wird vom unwirschen Erkennen der enormen Distanz zur wesentlich komplexeren Wirklichkeit. Diese Distanz ist dann auch von einem willigen Leser kaum zu überwinden. An diesen Punkt kamen bisher ausnahmslos alle Bücher über Mathematik, die ich gelesen habe, insofern ist es schade, daß auch Bewersdorff da keinen anderen Weg gefunden hat. Angesichts der sonst gebotenen Qualitäten sind das aber wirklich pingelige Kleinigkeiten. Insgesamt eine äußerst lohnende und rühmenswerte Lektüre für alle, die sich für Spiele interessieren und für deren mathematische Betrachtung offen sind. Lieber @Hans Dampf (von), besonders herzlichen Dank. Dein Hinweis brachte das Buch von meiner persönlichen "long list" zur sofortigen Lektüre. Volltreffer! Gruss elementaar

Hallo @Hans Dampf (von), Ha! Ja stimmt. Das kleine "aber" hat mit den unterschiedlichen Wahrscheinlichkeiten von "kommt nicht" (19/37) und "kommt" (18/37) zu tun. Diese eine Zahl mehr in den Wahrscheinlichkeiten ändert vieles, und mit steigender Spieldauer immer drastischer. Aus der Tabelle von weiter oben: Beispiel Länge 20: in der (Coup)zeit, in der wir eine 20er-Serie sehen, haben wir mit 882379/315874 schon 2,8 mal eine Nichttrefferserie derselben Länge 20 gesehen. Gruss elementaar

Hallo @Feuerstein, mit Freude bedanke ich mich für Deine enthusiastische Würdigung. Vielen Dank und das ist schön! Diese Passage hat mich besonders gefreut, zeigt die doch einen Geist, der vor logischen Konsequenzen nicht zurück schreckt, sondern ihnen mit dem erforderlichen Mumm begegnet. Denn das ist eine mögliche Konsequenz aus den vorgelegten Daten: wenn selbst ein solches Fiktivspiel nicht zum Kapitalisieren reicht, muss der Kapitalrückfluss bei Auszahlungen (man kann das auch Tilgungsraten nennen) zwangsweise größer werden, als es beim sich verdoppelnden Wachstum gegeben ist. Das ist wahrlich eine harte Nuss! Gruss elementaar

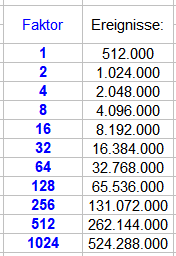
V Wieso nun diese Untersuchung? Wie in der Einleitung beschrieben ist das Bisherige, als Zahlenspäßchen mit der, wenn auch unvollständigen, Demonstration, was man damit anfangen kann, ein Nebenbeiergebnis einer ganz anderen Frage. Damals interessierte mich das (binär)logarithmische Wachstum, wie man es, in der Natur und anderswo, mannigfaltig beobachten kann. Bakterienstämme z.B. wachsen lange Zeit logarithmisch (mit jeder Zellteilung verdoppelt sich ihre Anzahl), das Wachstum findet jedoch sein "natürliches" Ende, wenn ihnen der Lebensraum ausgeht, was z.B. in einer Petrischale der Fall ist. Was würde man diesbezüglich mit der streng begrenzten Grundgesamtheit (die Zahlen 0 bis 36) des Roulettespiels und einem (rein fiktiven) Martingalespiel auf EC beobachten können? Daß dies im realen Spiel nicht funktioniert, durch den Grenzwertsatz gar nicht funktionieren kann, im Zweifel das reale Tischlimit die Grenze setzt - alles geschenkt. Es darf als bekannt vorausgesetzt werden. Der Link erklärt es im Zweifelsfall. Für mich war, ergebnisoffen, lediglich die Frage interessant, was wird man auf endlicher Spielstrecke beobachten können? Wie entwickelt sich der Gesamtsaldo der Veranstaltung, mit welchen Eskalationstufen an Ausbleibern hat man es zu tun, welche Rolle spielt die Zeit (in Coups gemessen), kurz: wie entwickelt und verhält sich ein solches System? Für einen derartigen Versuch darf es natürlich kein Tischlimit geben. Wenn ein Ausbleiber so lange auf sich warten läßt, daß man mehr Geld auf den Tisch legen müsste, als es Atome im Universum gibt, behilft man sich damit, daß der Bankhalter unbegrenzten Kredit gewährt und es genügt, als Einsatz auf einen Zettel 2^Fantastillion zu schreiben und auf den Tisch zu legen. Leider ist es mit dieser Festlegung aber noch nicht getan. Erforderlich sind auch noch zwei Grundannahmen: zu keinem Zeitpunkt während des Experiments darf nur noch "Zéro" erscheinen, und, damit im Zusammenhang aber nicht identisch: es muss nicht nur auf abzählbar endlicher, sondern auch real erlebbarer Spielstrecke jeweils einen Treffer für jeden Spieler geben. Sicher ist dies, siehe Kombinatorik, keineswegs. Wäre nur eine der beiden Grundannahmen während des Experiments verletzt worden, würde dies zum Abbruch geführt haben. Das Wachstum der Einsätze wäre zwar ungebrochen, mangels eines abschließenden Treffers der Sequenz aber, in der Wirkung wie "Unendlich", an sein "natürliches" Ende gekommen. Das war in dieser Stichprobe aber glücklicherweise nicht der Fall. Die erforderlichen Einsatzhöhen, um in jedem Versuch mit dem Ergebnis +1 Stück abzuschließen, wären gewesen: Der höchste kumulierte Einsatz für den 32er-Ausbleiber von knapp 4,3 Billionen Stück kann uns dabei gar nicht erschrecken - dafür findet sich bestimmt irgendwo noch ein Sondervermögen. Über die Umsatzrendite zum Gewinn des einen Stücks sehen wir ebenfalls großzügig hinweg. An (generalisierenden) Basisdaten fehlen jetzt noch "gespielte Coups" (Coupverbrauch), Umsatz und Gewinn/Verlustrechnung; in der folgenden Tabelle sind sie zu finden: In der letzten Zeile werden einige Spaltensummen gezogen. Wenn man 2.214.991.921 Coups spielt, kann man sich also über den Gewinn von 524.288.000 Stück freuen. Da jede der 524.288.000 Partien (alle Versuche) mit dem Ergebnis +1 Stück abgeschlossen wurde, ist es schön, daß auch rechnerisch ein Plus von 524.288.000 Stück herauskommt; daß damit eine irgend positive Umsatzrendite einher geht, ist ebenfalls nicht erstaunlich. Das ist ja Bestandteil der Versuchsbedingung. Eine Spur interessanter ist vielleicht, daß im oberen Teil der Tabelle alle Satzstufen, mehr oder minder stetig, ihre erwartbaren Minusprozent einfahren. Der erste wirkliche Gewinn wird (in dieser Stichprobe) erst in Satzstufe 21 erzielt. Die Satzstufen 1 bis 20 haben bis dahin nicht nur für eine gigantische Zeitverschwendung gesorgt (2.214.952.922 der insgesamt 2.214.991.921 und damit 99,9982% aller gespielten Coups!) Mit ihrer Tätigkeit haben sie auch ein Minus von 407.896.064 Stück angehäuft. Die zur Gesamtspielzeit noch fehlenden 38.999 Satzcoups müssen also nicht nur die angehäuften Verluste ausgleichen, sondern auch noch für den Gesamtgewinn sorgen: |-407.896.064| Stück + 524.288.000 Stück = 932.184.064 erforderliche Gewinnstück. Wobei die an sich positiven Satzstufen 21 und 22 sich nichts einbilden sollten, wird ihre Leistung doch von Satzstufe 23 mehr als aufgefressen. Wie dramatisch sich dies auswirkt, zeigt folgende Tabelle, in der die Satzstufenergebnisse kumuliert dargestellt sind: Das kann dann schon mal ernüchternd wirken: Der Gesamtgewinn von 524.288.000 Stück wird mit dem Satz auf den größten Ausbleiber dieser Stichprobe erzielt. Dafür mussten im letzten Satz in Coup 32 ganze 2.147.483.648 und damit kumuliert 4.294.967.295 Stück auf den Tisch gelegt werden. Dieser Befund ist nun wirklich fatal. Der ein oder andere Pfiffikus hat sich schon mal dem Gedanken gewidmet: bei dieser Sachlage spiele ich erst nach 20maligem Ausbleiben einer EC, und hat dabei, hoffentlich, zwei gravierende Denkfehler entdeckt: man beachte die Anzahl der gefundenen Ausbleiber: Ihre wenigen Exemplare verhalten sich genauso volatil und erratisch wie ein Gleichsatzspiel über wenige Coups. Sucht man aktiv nach ihnen, wird man bald mit noch größeren Ausbleibern konfrontiert - das hört nie auf (auch hier wieder Kombinatorik). das viel schwerwiegendere Problem ergibt sich allerdings daraus, wie der (im Fiktivversuch sichere Gewinn von einem Stück pro Partie) zustande kommt: er wird einzig aus dem partieabschließenden Treffer des jeweils aktuell größten Ausbleibers generiert. Und für diesen entscheidenden Treffer muss man mehr Geld auf den Tisch legen, als man jemals mit dem Spiel verdienen kann. Trotz sicherem +1 Stück pro Partie und trotz einer Umsatzrendite von 1,8%. Genau dies konnte ich während der Auszählung regelmäßig beobachten. Chronologisch befindet sich der Gesamtsaldo bei diesem Spiel sogar oft im Plus. Nähert sich der Gesamtgewinn jedoch einer (sehr breiten) Zone, in der ein intuitiv (natürlich meistens falsch) erwarteter neuer größter Ausbleiber erscheinen könnte, dauert es nicht lange, bis der Saldo steil ins Minus abbiegt, und nur durch den letztendlichen Treffer wieder aufgepäppelt wird. Jegliches Kapitalisieren wird so vollkommen unmöglich. Und das bedeutet: selbst in einem Fiktivspiel mit sicherem Gewinn (solange obige Grundannahmen zutreffen, was nicht sicher ist!) von einem Stück pro Partie, bleibt man Gefangener des negativen Erwartungswertes des Spiels und seiner Spielregeln, und muss mehr Geld mitbringen, als man jemals damit verdienen kann. Da mag jetzt der ein oder andere echte Mathematiker vor Lachen unter dem Tisch liegen, kann man sich das Verhalten eines solchen Systems doch recht einfach herleiten - da lache ich herzlich und vorbehaltlos mit und sage nur: jeder, wie er halt kann. Wer's nicht in der Birne hat, muss eben die Ochsentour machen. Gruss elementaar

Hallo @Hans Dampf (von), Ach was, bitte mach Dir darüber keine Gedanken. Meine gelegentlichen öffentlichen "Verzweiflungs"bemerkungen sind Ausdruck von: "ich bemühe mich weiter, es zu erklären, mir gehen aber so langsam die Varianten aus". Solange es auf begründbare Fragen eine Antwort gibt, und man diese kennt, muss man sich eben so lange bemühen, bis es dem Fragesteller einleuchtet. Ich wüsste nicht, wie es anders gehen könnte. Danke @Spielkamerad. Tatsächlich bereite ich gerade einen Beitrag vor, der die Schraube in gewisser Weise noch ein wenig weiter dreht, dabei aber das Thema erweitert. Dauert aber noch eine kleine Weile. Gruss elementaar

Hallo @Hans Dampf (von), Unter der Voraussetzung, daß man keine fremden Stücke klaut, daß man sich also an die Spielregeln hält - und das sollte bei jedem Spiel absolut gesetzte Ehrensache sein - ist das unmöglich; ganz humorlos, keinerlei Spielraum für "Glauben". Mit Zéroteilung kann man den Verlust pro Coup zwar auf durchschnittlich 0,514 Stück reduzieren, das ist aber der Spielregel und weniger der Satztechnik geschuldet. So wie es gekommen ist, zweifellos! Das war insofern eine heftige Fehleinschätzung von mir, wobei das Wort "Fehleinschätzung" die dahinter stehende Tatsache eher verschleiert als sie benennt. Jeder hat halt seine eigenen Verständnisstrukturen und blinde Flecken. Das Erkennen des kombinatorischen Charakters (nicht nur) des Roulettespiels, erlebte ich, über vierzig Jahre ist es her, als einen der seltenen Momente der Klarsicht innerhalb von Bruchteilen einer Sekunde; in den Sekunden danach eine ganze Reihe von Folgen, die sich daraus ergeben, schneller als ich gemeinhin denken kann. Es war ein Moment, wo sich der "Schleier der Maya" einen kurzen Moment für mich gelüftet hat - am recht profanen Objekt, klar, aber immerhin. Weil ich außerdem die Kombinatorik in früheren Beiträgen schon gelegentlich erwähnt habe, glaubte ich, mich diesmal auf Knappheit beschränken zu können. Das jemand darin eine "Rückoptimierung" erkennen könnte, wäre mir aber auch mit größerer Ausführlichkeit sicher nicht eingefallen. Das ist mein blinder Fleck: was, begründbar, gar nicht da ist, darum kümmere ich mich auch nicht. Das Antworten auf Deine Nachfragen mag zwar ab und zu etwas anstrengend werden, das ist aber überhaupt kein Gegenargument. Im Gegenteil: es bringt doch rein gar nichts, bestehende Unklarheiten, wenn möglich, nicht aufzuhellen. Da könnte ich das Verfassen von öffentlichen Beiträgen ja gleich sein lassen. Deshalb ist Dein beharrliches und begründetes Nachfragen jederzeit willkommen - als pure Selbstverständlichkeit für mich sowieso nicht hinterfragbar. Gruss elementaar

Hallo @Hans Dampf (von), Oh ja. Wenn Du alle 37 Scheinspieler real mit gleichem Stückwert setzt, hast Du die Schwankungen ultimativ besiegt. Jeder Coup ergibt schwankungslos das Ergebnis -1 (ohne Tronc). Es war als Verständnishilfe für die Aussage gedacht, daß der größtmögliche Ausbleiber so lange wie die betrachtete Coupsstrecke ist. Es sollte außerdem die Relativität der Berechnung von Standardabweichung und Signifikanz verdeutlichen. Daß das reale Erscheinen des größtmöglichen Ausbleibers mit längerer Coupsstrecke immer unwahrscheinlicher wird, habe ich in der Einleitung beschrieben, weiter oben vorgerechnet und ist, mittelbar, Gegenstand der Auszählung. Gruss elementaar

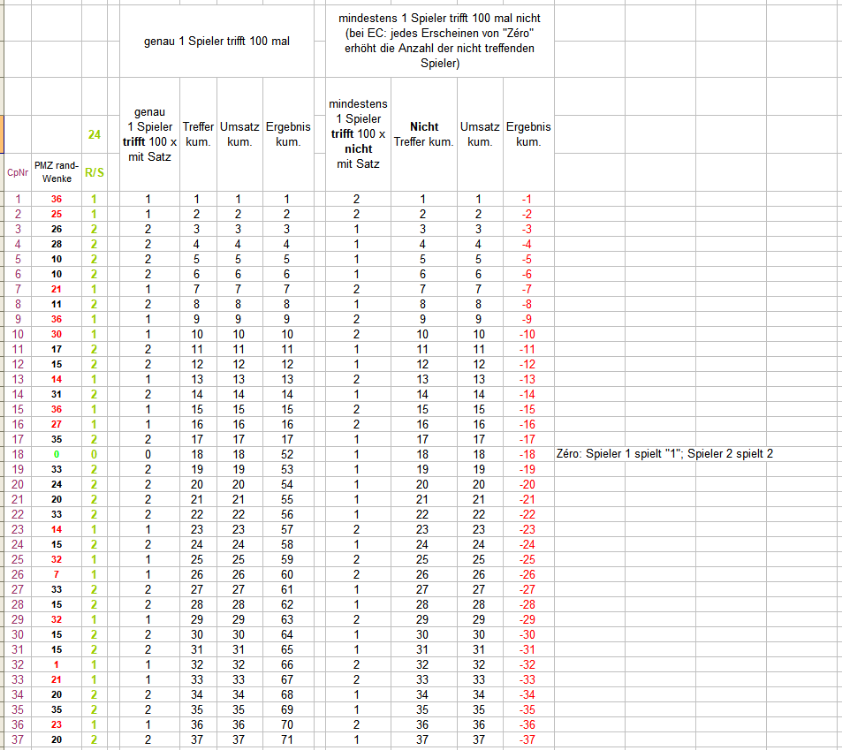
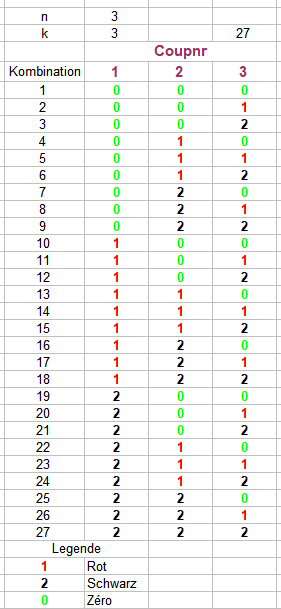
Hallo @Hans Dampf (von), Da ich Deine Fragen schon mehrfach beantwortet habe, fürchte ich, daß wir so nicht weiterkommen. Indem er eine der beiden möglichen EC setzt. Seherfähigkeiten sind ganz überflüssig - es geht um Kombinationen. Mir fällt jetzt nur noch ein Schritt-für-Schritt-Vorgehen ein. Irgend ein "Rot"-"Schwarz"-Spieler soll drei Coups spielen. Er kann sich in jedem Coup neu entscheiden ob er "Rot" oder "Schwarz" setzt. Im ersten Coup kann entweder "Rot" oder "Schwarz" oder "Zéro" (n = 3) erscheinen. Mehr Möglichkeiten gibt es für sein Spiel nicht. Möchtest Du das bestreiten? Im zweiten Coup kann entweder "Rot" oder "Schwarz" oder "Zéro" (n = 3) erscheinen. Mehr Möglichkeiten gibt es für sein Spiel nicht. Möchtest Du das bestreiten? Im dritten Coup kann entweder "Rot" oder "Schwarz" oder "Zéro" (n = 3) erscheinen. Mehr Möglichkeiten gibt es für sein Spiel nicht. Möchtest Du das bestreiten? Listet man vollständig jeden überhaupt nur möglichen Permanenzverlauf für drei Coups und ein beliebiges EC-Spiel auf, erhält man die oben schon gezeigte Tabelle: In drei Coups kann dreimal "Zéro" kommen. In drei Coups kann dreimal "Rot" kommen. In drei Coups kann dreimal "Schwarz" kommen. In drei Coups kann jede überhaupt nur mögliche Mischung aus den drei Elementen "Rot" oder "Schwarz" oder "Zéro" kommen. Die Tabelle listet vollständig alle Möglichkeiten auf. Zu etwas anderem ist der Roulettezufall nicht in der Lage. Möchtest Du das bestreiten? Auf drei Coups kommen mit "Rot", "Schwarz" und "Zéro" genau 27 mögliche Kombinationen heraus. Bringen wir also 27 Scheinspieler an den Start, jeder bekommt drei Satzstücke und muß jeweils eine der gelisteten Kombinationen für drei Coups als "Marsch" setzen. Spieler 1 muß dreimal "Zéro" setzen (Vorauswissen ist dafür nicht nötig) - erscheint jetzt dreimal "Zéro", hat er (als einziger = genau) dreimal gesetzt und dreimal getroffen. Gleichzeitig haben die Spieler, deren vorgeschriebener "Marsch" kein Setzen von "Zéro" vorsieht mit der gleichen Permanenz null mal getroffen, also dreimal hintereinander nicht getroffen. Im Beispiel (dreimaliges Erscheinen von "Zéro") haben die Spieler 14, 15, 17, 18, 23, 24, 26, 27 alle null mal getroffen. (Mindestens = ">=1"). Spieler 12 muß (ohne jedes Vorwissen, marschgemäß) in Coup 1 "Rot" setzen, in Coup 2 "Zéro" und in Coup 3 "Schwarz". Erscheint jetzt die Permanenz "Rot", "Zéro", "Schwarz", hat er (als einziger = genau) dreimal gesetzt und dreimal getroffen. Im diesem Beispiel (Permanenz ist "Rot", "Zéro", "Schwarz") haben die Spieler 4, 5, 7, 8, 22, 23, 25, 26, 27 alle null mal getroffen. (Mindestens = ">=1"). Irgendein Vorauswissen ist vollkommen überflüssig. Man lege so viele Scheinspieler an, wie es, auf Coupsstrecke und Chancengröße bezogen, Kombinationen gibt, und erhält damit (auf abzählbarer Strecke) nicht nur die genaue Anzahl an Möglichkeiten, wie eine Permanenz überhaupt nur aussehen kann, sondern auch, was jeder Scheinspieler zu setzen hat. Und unter diesen Scheinspielern gibt es genau einen, der alles richtig gemacht hat, und mindestens einen, der alles falsch gemacht hat. Gruss elementaar PS: Ob vorwärts oder rückwärts ist vollkommen unerheblich. Ab jetzt vorwärts gespielt, muß eine von 27 Kombinationen auf drei Coups dreimal treffen. Ab jetzt drei Coups rückwärts betrachtet, hat ebenfalls genau eine von 27 Kombinationen auf drei Coups dreimal getroffen. Geht auch rollierend, gestückelt oder was man sich noch ausdenken mag.

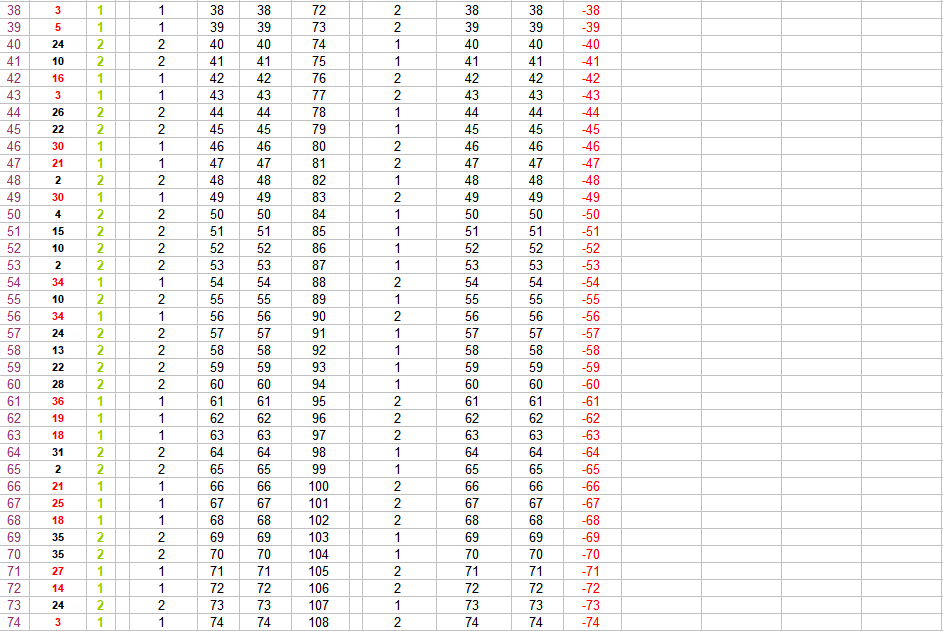
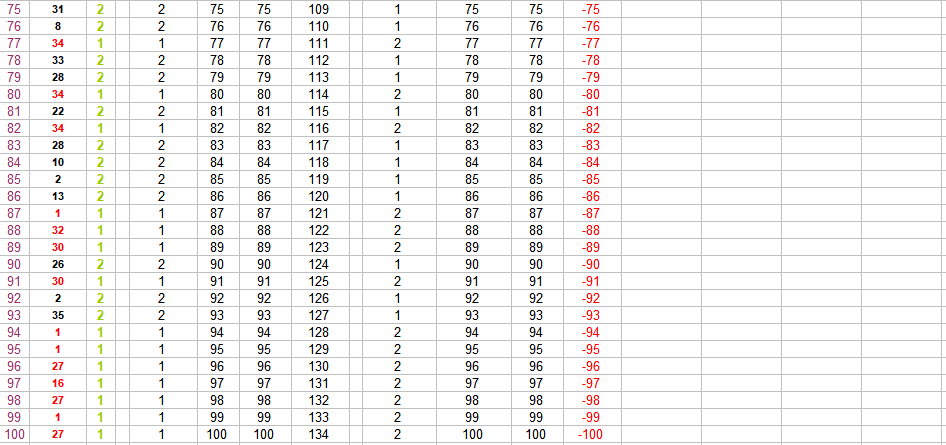
Hallo @Hans Dampf (von), gestern Abend das Finale der Snooker Tour Championship: zwei großartige Meister ihrer Zunft bei der Arbeit - phantastisch! Auf 100 Coups haben beide 100 mal gesetzt und damit "100 Zahlen gespielt" Wenn man unbedingt (in diesem Zusammenhang) spitzfindig sein will, spielt ein EC-Spieler natürlich die Chancengröße 18/37. Mindestens ein Spieler, der 100 mal nicht trifft, setzt 100 mal die EC, die nicht erscheint. Mit jedem Erscheinen von "Zéro" erhöht sich die Anzahl der 100 mal nichttreffenden Spieler, weil man, um "Zéro" nicht zu treffen, sowohl "Rot" als auch "Schwarz" setzen kann. Die nichttreffenden Spieler setzen also jeder 100 mal 18 Zahlen. Genau ein Spieler trifft 100 mal, weil er alles richtig gemacht hat: erscheint eine der beiden EC, hat er die EC gesetzt, die auch ercheint und trifft. immer wenn "Zéro" erscheint, hat er just dort "Zéro" gesetzt und trifft. Die genaue Anzahl gesetzter Zahlen, hängt damit bei ihm von der Häufigkeit des Erscheinens von "Zéro" ab. In der Beispielpermanenz erschien auf 100 Coups lediglich einmal "Zéro" also setzte der hier 100 mal treffende Spieler 99 x 18 + (1x 1) Zahl. Im Durchschnitt wird er wohl mit knapp dreimaligem Erscheinen von "Zéro" auf dieser Spielstrecke zu rechnen haben; gesetzte Zahlen wären dann 97 x 18 + (3 x 1) Zahlen. Beispielpermanenz (auf 100 Coups muss gestückelt werden, Du hast aber auch Wünsche!) Gruss elementaar

Hallo @Hans Dampf (von), Mit einem gewissen Recht! (Danke für die Erläuterung und den Link). Meine Aussage ist aber eine andere als der Gedanke von @charly22. Die Analogie, die Du siehst, existiert gar nicht. Bespiele ich für drei Coups ein EC-Paar (18/37 + 18/37 + 1/37) existieren folgende, und nur diese Möglichkeiten: Nicht mehr und nicht weniger. n = 3 (Rot, Schwarz, Zéro) k = 3 (Coup Nr 1, 2 ,3) Alle möglichen Kombinationen = n^k = 27 Egal welche Permanenz real erscheint, es läßt sich mindestens ein Spieler (eine Kombination) finden, der dreimal nicht trifft und genau einen der dreimal trifft. Bespiele ich neun Coups mit n = 3 (Rot, Schwarz, Zéro) dann ist k = 9 (Coup Nr 1, 2 ,3, 4, 5, 6, 7, 8, 9) und alle möglichen Kombinationen sind n^k = 19.683 Bespiele ich 50 Coups mit n = 3 (Rot, Schwarz, Zéro) dann ist k = 50 (Coup Nr 1, 2 ,3, ... 50) und alle möglichen Kombinationen sind n^k = 717.897.987.691.853.000.000.000 Bei 100 Coups mit n = 3 (Rot, Schwarz, Zéro) ist dann k = 100 (Coup Nr 1, 2 ,3, ... 100) und alle möglichen Kombinationen sind n^k = 515.377.520.732.011.000.000.000.000.000.000.000.000.000.000.000 Klar, besonders die beiden letzten Zahlen sind gigantisch groß - aber abzählbar, darauf kommt es an. Aber auch hier: egal welche Permanenz real erscheint, es läßt sich mindestens ein Spieler finden, der 100 mal nicht trifft und genau einen der 100 mal trifft. Und zu mehr ist der roulettespezifische Zufall auch nicht in der Lage, durch die strikte Begrenzung auf 37 überhaupt nur mögliche Zahlen. Gruss elementaar

Hallo @Hans Dampf (von), Ich muß wohl von einer, hoffentlich nur temporär bestehenden, ganz besonders ausgeprägten Vernageltheit meinerseits ausgehen. Ich verstehe den Satz nämlich schon wieder nicht. Was ist es denn, was nichts mit "EC - Die größten Ausbleiber" zu tun hat? Die Kombinatorik gilt natürlich für alle Chancengrößen, inklusive der Einfachen Chancen. Pro Chancenpaar muss man dann drei Teile verteilen (bspw. "Rot", "Schwarz" und "Zéro"). Das macht man dann für eine beliebig lange, aber abzählbare Spielstrecke und erhält damit sämtliche, überhaupt nur möglichen Ergebnisse, wie eine Permanenz sich entwickeln könnte. Und darunter ist immer mindestens eine Kombination (als Scheinspieler oder "Marsch" aufgefasst), die auf einer beliebigen Permanenzstrecke beliebiger aber abzählbarer Länge keinen einzigen Treffer erzielt. In wie fern hat das nichts mit der Themenüberschrift zu tun? Gruss elementaar

Hallo @Hans Dampf (von), vielen Dank, jetzt hab' ich's verstanden. Das Wort "Kombination" habe ich im Sinne der "abzählenden Kombinatorik" verwendet - da muß man nicht nur die verwendeten Teile (was denn "kombiniert" werden soll), sondern auch die Länge der Betrachtungsstrecke vorher angeben. Schönen Restsonntag! Gruss elementaar

Hallo @Hans Dampf (von), zu diesem Gedankenkunststück muss ich um Erläuterung bitten. Was ich, als Verständnishilfe, schrieb, war: betrachte die letzten 100 tatsächlich erschienenen Coups; spiele virtuell von Coup 1 bis Coup 100 etwas anderes als tatsächlich erschienen ist; erhalte damit mindestens einen Scheinspieler (Marsch), der eine 100er Fehltrefferserie hingelegt hat. Hätte man sich vor Coup 1 die Mühe gemacht, sämtliche überhaupt nur möglichen Kombinationen (wahrscheinlich in Googol-Größe) aufzuschreiben, würde man mindestens eine Kombination finden, die genau 100 mal nicht trifft. Gruss elementaar

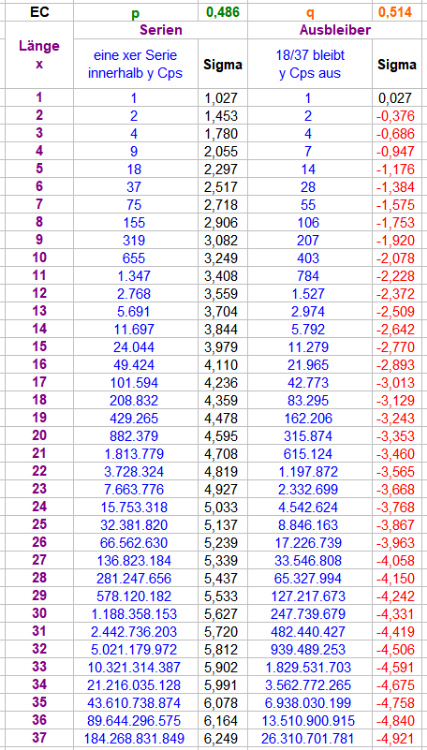
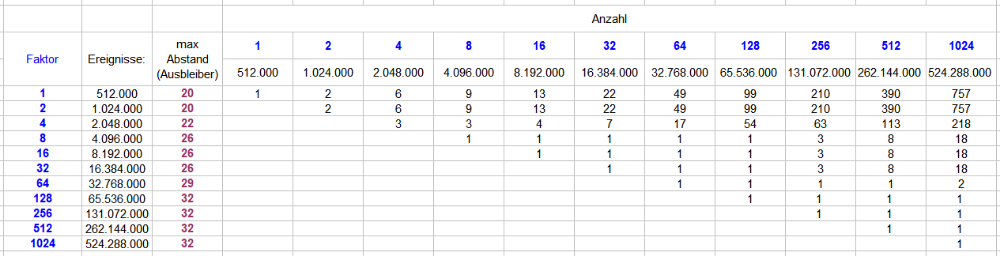
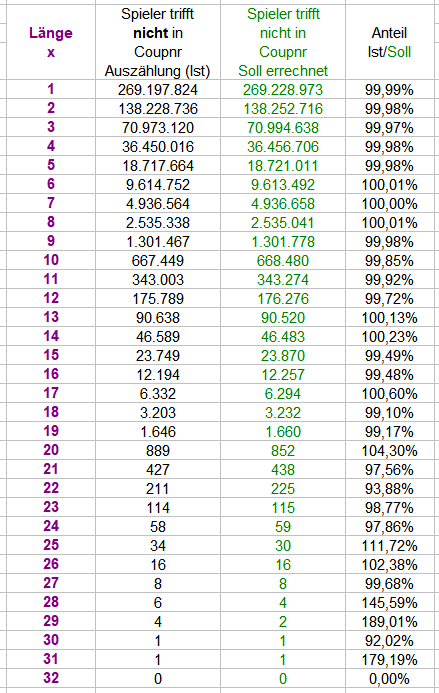
IV Noch ein Addendum Es könnte noch interessieren, wie sich die größten Ausbleiber im Verlauf der Gesamtauszählungsstrecke entwickelt haben. Nach 512.000 Versuchen gab es einen Maximalausbleiber von "20" (d.h. ein Spieler hat erst im 20. Versuch getroffen). Nach der doppelten Menge an, nämlich 1.024.000, Versuchen gab es keinen neuen Maximalausbleiber, dafür erschien Ausbleiber "20" zweimal. Wie schwankungsstark dieses Ausbleibersuchen ist, kann man sich nun mit Rechenspielchen egal ob von links nach rechts oder von rechts nach links verdeutlichen. Bleiben wir bei Ausbleiber "20": die ersten beiden Werte könnten Stetigkeit suggerieren: innerhalb von 512.000 Versuchen erscheint ein Ausbleiber der Größe "20". Beispielhaft hier: Nehmen wir die scheinbare Stetigkeit aus den beiden ersten Portionen für bare Münze, müssten am Ende ganz rechts ungefähr 1024 Exemplare mit dem Erscheinensabstand "20" gezählt worden sein. (Erste grüne Zeile, Faktor 2). Es sind aber nur 757 Exemplare gesichtet worden. Die zweite grüne Zeile (Faktor 1/2) geht den umgekehrten Weg: nehmen wir 757 am Ende der Auszählung als aussagekräftig an, ist die Rückwärtsentwicklung nicht überzeugender. Macht man dieses Hin- und Herrechenspielchen über die gesamte Tabelle, wird man vermuten können, daß Erscheinensabstand "32" recht früh erschienen ist, und Abstand "22" (in 4). mit gleich drei Exemplaren, vielleicht etwas spät. Was sagt uns dazu eigentlich eine errechnete Tabelle? Ein 20er-Ausbleiben hätten wir danach innerhalb von 315.874 Versuchen erwarten können, ein 22er-Ausbleiben innerhalb von 1.197.872 Versuchen ein 32er-Ausbleiben innerhalb von 939.489.253 Versuchen. Nebenbei ein Beleg dafür, welch irrige Vorstellung das Gerede von "alle x Coups erscheint..." etabliert. Den oben erwähnten, selbst erlebten 26er-Ausbleiber, hätte ich innerhalb von 17.226.739 erlebten Versuchen erwarten dürfen. "Innerhalb" war es zweifellos, für Durchschnittszahlenfreunde aber doch recht früh, "unverdientes" Glück eben. Jetzt setzen wir die errechneten Werte dieser Tabelle noch ins Verhältnis zu den real aufgefundenen Werten der Auszählung und erhalten: Mindestens als nachträgliche Plausibilitätsprüfung sollte das genügen. Und als kleine Erinnerungshilfe, daß richtiges Rechnen zweifellos wichtig ist, in der reinen Anschauung aber zuweilen ein höherer Erkenntniswert steckt. Gruss elementaar

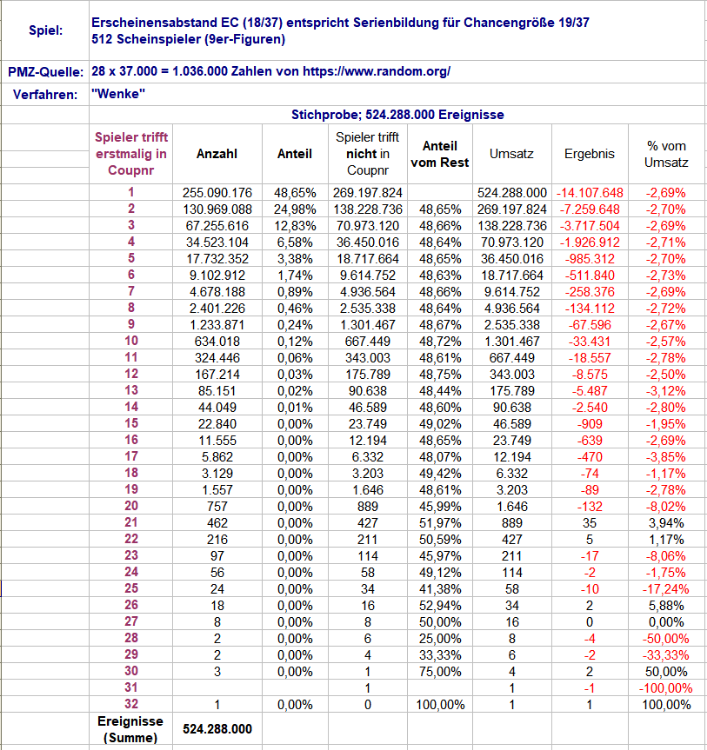
III Ergebnis Ich möchte hoffen, die Tabelle sei selbsterklärend. Falls dennoch eine Lesehilfe erwünscht ist, bitte ich um Nachfrage. Ganz rechts ist der Bankvorteil mit 1/37 angegeben, für EC-Spiele mit Zéroteilung muss er halbiert werden. Damit kann die eingangs gestellte Quatschfrage für diese Stichprobe beantwortet werden: Unter den 512 Spielern gab es einen Pechvogel der ein 31-maliges Nichttreffen hinnehmen mußte und erst im 32. Versuch zu seinem ersten Treffer kam. Bemerkenswert deutlich in dieser Stichprobe: erwartbar heftiger werden die prozentualen Schwankungen, je weniger Ereignisse spezifischer Qualität angetroffen werden. So produziert bspw. Trefferabstand "12" mit 167.214 (!) gefundenen Exemplaren zu diesem Zeitpunkt immer noch eine Schwankung in der ersten Nachkommastelle. selbst bei einer Gesamtereignisgröße von einer halben Milliarde, bekommt man zuweilen den prozentualen Erwartungswert der Chancengröße 18/37 noch nicht einmal für die zweite Nachkommastelle stabil. kleine Schwankungen im Erscheinenswert bewirken etwas größere Schwankungen in der Umsatzrendite (Rundungsfehler unberücksichtigt). sehr schön auch zu sehen, welche "Umsatzschuld" schon ein zweiter Satz auf EC wieder wettmachen muss, falls der erste Satz nicht getroffen hat. Das Wort "Stichprobe" betone ich deshalb so, weil Schwankungen eben auch bedeuten, daß eine weitere Stichprobe mit einer halben Milliarde Ereignissen differierende Ergebnisse zeigen wird.

II Methode Zur Zeitersparnis ist das Anlegen von parallel agierenden Scheinspielern angezeigt. Ein einfaches Verfahren zum Erschaffen von Scheinspielern ist das spaltenweise Buchen von "Folge" und "Wechsel". Ein Nachteil ist dabei, daß man einen Permanenzvorlauf in der Größe der anzulegenden Scheinspieler benötigt. Deshalb kam ein anderes Verfahren zur Anwendung. Kombinatorisch ergeben sich auf neun Coups 2^9 = 512 (siehe vdW) Scheinspieler. Nach neun Coups setzt jeder Scheinspieler wieder mit dem Anfang seiner Sequenz weiter. Als zu untersuchende Spielstrecke habe ich 100 Coups festgelegt. Würde ein noch größerer Ausbleiber aufgetaucht sein, würde dies unter der Zahl "101" unspezifisch summiert werden; glücklicherweise war das aber, in dieser Stichprobe, nicht der Fall. Gezählt wurde für alle 512 Scheinspieler der Coup des ersten Treffers. Damit es bei angepeilten >500 Mio. Ereignissen mit Verfahren "Wenke" nicht doch zu einer Generatorunwucht kommt, habe ich 28 x 37.000 = 1.036.000 Zahlen von random.org/ zur Permanenzerzeugung benutzt. Pro frisch erzeugter Permanenz von 100 Coups Länge konnten so 512 Ereignisse gezählt werden. Anders als bei Auszählungen, wo ein unmittelbar praktischer Nutzen unterstellt wird, habe ich die Portionsgrößen nach diesem Prinzip eingeteilt. Ein Photograph wird sofort eine Blendenreihe erkennen - es ist eine einfache logarithmische Reihe zur Basis 2 Der Grund dieses Vorgehens wird weiter unten deutlich werden.

Nach 971 Beiträgen in diesem Forum, mache ich zum ersten Mal ein Thema auf. I Einleitung Vor vielen Jahren mal in einer Korrespondenz mit @Egoist erwähnt, habe ich kürzlich die Datei wiedergefunden, in der ich in einer Stichprobe von über einer halben Milliarde Versuchen als Nebenprodukt nach dem größten Ausbleiber der Chancengröße EC (18/37) gefragt habe. Diese Datei habe ich jetzt ein wenig aufpoliert und präsentabel gemacht. Die Frage an sich ist natürlich naiv, denn die allgemeingültige Antwort lautet: der größtmögliche Ausbleiber ist gleich der Coupstrecke, die man betrachtet. Das gilt ebenso für die Länge von Trefferserien. Diese intuitiv vielleicht nicht einfach begreifbare Tatsache muss man akzeptieren; z.B. indem man sich den kombinatorischen Charakter des Roulettespiels in Erinnerung ruft. Eine streng begrenzte Menge überhaupt nur möglicher Ereignisse, nämlich die Zahlen 0 bis 36, führt bei jeder abzählbaren Menge an Coups zu einer zwar stark steigenden, aber immer noch abzählbaren Menge an überhaupt nur möglichen Kombinationen. Dadurch, daß für den nächsten Coup die prozentuale Gleichwahrscheinlichkeit der möglichen Ereignisse postuliert wird (nämlich eine aus 37 möglichen Zahlen), wird auch die prozentuale Gleichwahrscheinlichkeit aller daraus folgenden Kombinationen deutlich. Läßt sich die prozentuale Gleichwahrscheinlichkeit von Kombinationen im Experiment nicht verifizieren, deutet dies auf eine Störung des Zufallsgenerators hin. Der kombinatorische Charakter des Roulettespiels verdeutlicht so nebenbei auch, daß die Ergebnisse der Berechnungen zur Standardabweichung und Signifikanz lediglich relativ und nicht absolut sind. Trotz Gleichwahrscheinlichkeit wird man nun nicht erwarten können, jemals auf 100 Coups das Erscheinen von 100 x "Rot" zu sehen. Das ist aber ein Problem menschlicher Wahrnehmung und hat mit Wahrscheinlichkeiten nur insofern zu tun, als es eben kaum erfassbar viel wahrscheinlicher ist, daß etwas anderes kommt als ausgerechnet 100 x "Rot". Ein weiterer Verständnistrick ist, einfach die letzten 100 Coups zu betrachten und sich zu verdeutlichen, daß es zu dieser konkreten, nicht bestreitbaren Kombination mindestens eine gibt, die 100 mal nicht getroffen hat. Sucht man danach, sind auch winzige Wahrscheinlichkeiten nicht so selten, wie es die errechneten Bruchteile suggerieren. Die längste selbst erlebte Ausbleiberstrecke habe ich übrigens Anfang der 1990er Jahre in Dortmund-Hohensyburg gesehen: dort blieb "Rot", wenn ich mich richtig erinnere, 26 mal aus. Die menschliche Wahrnehmung mit "das gibt's doch gar nicht" und "jetzt muss doch..." führte zu zentimeterhohen Jetonstapeln im gesamten Setzfeld von "Rot" und relativ bescheidenen Einsätzen auf "Schwarz". Da "Schwarz" mehrmals durch "Zéro" gestört wurde, hielten sich die Gewinne der "Schwarz"spieler in Grenzen, die Verluste der "Rot"spieler waren astronomisch - insgesamt eine spektakulär einträgliche Spielstrecke für die Bankhalter.

Hallo @Das Kuckuck, obwohl Dein Beitrag an einen Anderen gerichtet, und weil mein Forenname fiel, stelle ich noch einmal, explizit und hoffentlich unüberlesbar, fest: unsere Sichtweisen auf Zufallsgeschehen unterscheiden sich stark. Was soll daran schlimm sein? Erstaunt hat mich allerdings Dein Zutrauen, öffentlich Feststellungen darüber zu treffen, wer welche Kenntnisse hat. Falls Du Erkenntnisse aus Naturanalogien ziehst - Glückwunsch; aber ich kann und will zu diesem Gebiet nichts beitragen. Für meine Betrachtungsweise ist das einfach kontraproduktiv und nicht zielführend. Ich bin auch am "Wesen" des Zufalls nicht interessiert, sondern, und das fast ausschließlich, an seinen Erscheinungsformen. Bei meinen Methoden würde sich das "Wesen" des Zufalls auch nur als unfallartiger Beifang "enthüllen", und bei mir zunächst heftigstes Misstrauen in die Durchführung des Experiments hervorrufen, nämlich ob auch wirklich mit größtmöglichem Zufall operiert wurde. Gibt es eine starke Wenn-Dann-Beziehung, kann es kein Zufall mehr sein. Viel mehr muß ich darüber für mein Interessengebiet nicht wissen. Dagegen ist das Studium der Erscheinungsformen, und, nicht ganz unwichtig, was sich daraus nichtzufällig machen läßt, sowohl im praktischen Spiel wie im Experiment bis jetzt ein immer noch wirksames Faszinosum. Dabei möchte ich es mal belassen. Gruss elementaar

Hallo @Das Kuckuck, Dein Beitrag liest sich, wie oft, sehr amüsant, läßt mich aber doch auch ratlos zurück. Gibt es darauf überhaupt eine sinnvolle Antwort? Den Spott im Fussballvergleich und dem ach so beliebten Küchentisch, nehme ich wohl wahr; was aber habe ich damit zu tun? In meiner Küche steht gar kein Tisch und der Raum wird ausschließlich zur Herstellung möglichst wohlschmeckender Speisen verwendet. Und Fußball interessiert mich wörtlich null. Außer der methodischen Unvereinbarkeit mit dem Roulettespiel kann ich dazu nichts weiter feststellen. Deiner zentralen Zusammenfassung der Aussagen von @Bold Player: stimme ich nicht zu, und es ist schade, wenn Du das tatsächlich so siehst. Vielleicht wirst Du aber einräumen, daß Deine nicht die einzig mögliche Zusammenfassung ist. Zumal ich sie auf mich sowieso nicht beziehen kann. Auf abstrakter Ebene (und dafür logisch einwandfrei) habe ich schon mehrmals, und zwar explizit, geschildert, was eine Strategie zur Gewinnfähigkeit mindestens leisten muß, und damit auch, wohin man konkret zu blicken hat. In vielen, zugegeben verstreuten, Nebensätzen habe ich Hinweise gegeben, wie so ein Blick aussehen könnte. Die wahrscheinlich allermeisten meiner Beiträge beschäftigen sich in belegter, hoffentlich nachvollziehbarer Ausführlichkeit mit der Frage, was und wie es NICHT geht. Daraus die entsprechenden logischen Schlüsse zu ziehen, ist in meinen Augen keine unbillige Forderung an einen interessierten Leser. Das ist, wieder in meinen Augen, sehr viel mehr als "nichts" oder Heimlichtuerei aus undurchsichtigen Motiven. Und die "Lösung", die @Bold Player herleitet (und eben nicht so einfach hinschreibt), nämlich das intensive Studium von Permanenzen und dem Ziehen der richtigen Schlüsse, ist eine Arbeit, die jeder für sich tun muss. Eine Abkürzung ist mir nicht bekannt. Daß es überhaupt eine geben könnte, erscheint mir sehr unwahrscheinlich (10.000 Stunden Faustregel). Und wer das nicht will, der läßt es eben bleiben. Da besteht gar kein Zwang. Um doch noch in die Küche zu gehen: es ist eine Frage des Qualitätsniveaus (sowohl des Rezept schreibenden Kochs als auch des Lesers), wie umfangreich und am Ende aussichtslos das Schreiben eines einzigen Rezepts manchmal sein kann. Mit der Aufzählung der Zutaten (womöglich auch mit Mengenangaben) und nachfolgender Schilderung der chronologischen Verarbeitungstaten ist es nicht getan. Fängt man an, die Chronologie der Taten auf das jeweilig konkret vorliegende Garverhalten der Naturprodukte zu beziehen, wird klar, welchen Erfahrungsschatz eines aufgeweckten und erfahrenen Kochs man voraussetzen muss, um nicht im endlosen Buchstabennirvana zu landen, bei denen Leute "nicht vom Fach" sowieso kaum noch etwas verstehen könnten. Derartiges fürs Roulettespiel wird es allerdings von mir sicher nicht geben. Das ist noch nicht einmal böser Wille oder phantasierte Angst vor Gegenreaktionen der Bankhalter, es ist mir schlicht zu viel Arbeit. Gruss elementaar

Hallo @Zecke, mit voller Zustimmung und großem Respekt lese ich den Beitrag von @Bold Player, der aus meiner Sicht ganz großartig ist. Für das von ihm erwähnte "Studium der Permanenzen" hat sich für mich als äußerst hilfreich erwiesen, mir für jede Strategie ein sich entwickelndes "Mäusekino" aufzusetzen, beispielsweise für Saldoverlaufskurven. Das mache ich parallel einmal chronologisch (Coup für Coup, wie man es am Spieltisch erleben würde), und gleichzeitig rollierend (für den neuesten Coup fliegt hinten einer raus). Beim ersten Diagramm lautet die Frage: was kann man als Spieler zum jeweiligen Zeitpunkt wissen? (Kombinatorik: mindestens einen fiktiven Spieler gibt es, der auch den nächsten Coup richtig vorhersieht, und weitergehend: die nächsten paar Coups überwiegend richtig setzt. Welche Fiktivspieler sind das?) Beim zweiten Diagramm wird deutlich, wie es einem Spieler ergangen wäre, der mit derselben Strategie früher angefangen hätte. Beide Diagramme zusammen sind Hilfsmittel, um die Frage besser beantworten zu können: wiederholt sich etwas in dem gerade betrachteten Permanenzstück, oder entwickelt sich etwas Neues? Als zweites hätte ich noch eine vermeintliche Banalität: in Deinem Nasenbeispiel (deutlich unterkomplex weitergeführt), nehmen wir an, Du hättest, aus welchen Gründen auch immer, ein Stück auf Fortsetzung der Nasenwiederholung gesetzt und dieses wäre weggeflogen, sprich: hätte nicht getroffen. Das ist eine geldbeutelwirksame Tatsache, auf die man wirksam reagieren muss! Gerade bei EC (18/37) ist ein wegfliegendes Stück ein so heftiges Statement der Permanenz, daß man ihm unüberlegt kein weiteres hinterher werfen sollte. Ich möchte betonen, für mich (!) hat sich das Geschilderte als hilfreich erwiesen. Wie es Anderen damit ergehen könnte, kann ich nicht beurteilen. Gruss elementaar

Schreiben kannst du auch nicht ? Finde den Fehler! https://de.wiktionary.org/wiki/Fantastillion https://mint-zirkel.de/2025/02/fantastillion/ https://www.zackbum.ch/2022/06/10/fantastillionen/ https://www.rechner.club/zahlwort/zahlnamen-tabelle

Angemaßtes Wissen, welches ER objektiv gar nicht haben kann. Mein Interesse am Hantieren mit Spielgeld erlahmte etwa im Alter von sechs oder sieben Jahren für immer. Noch so intensives Hantieren mit Fantastillionen von Spielgeld führen nicht zu profunden Kenntnissen in Buchhaltung. Der Glaube es sei doch so, führt, wie ER gerade demonstriert, zu schwerwiegenden Beurteilungsfehlern in der Frage was wann wichtig ist. SEIN Erfindungsreichtum im Produzieren von himmelschreiendem Unfug sei ungebrochen, ich jedenfalls brauche jetzt mal eine Pause.

Und wird genau deshalb zur, hoffentlich wenigstens richtig gerechneten, vollkommen sinnlosen Zahl, die ohne Zusatzinformation nichts aussagt (außer, daß ER sie errechnet hat). @Ropro hat es gerade in einfachster Sprache erklärt. Schon mal das Wort "Umlaufvermögen" gehört? Buchhaltung kann ER also auch nicht. Hanebüchen.

Soll das der Versuch einer Selbstcharakterisierung sein? Das schon längst geplatzte Phrasenschwein ist jedenfalls immer noch aufnahmefähig. Wie ich kürzlich von einem der Multilutschers erfahren habe, ist das Bestehen darauf, daß zwei nicht drei und auch nicht vier ist, "unerträgliche" "Korinthenkackerei". Daß es für sie und ihren Geistesbruder wörtlich "unerträglich" wäre, bleibt dabei wohl eine Hoffnung, die sich sicher nicht erfüllen wird. Es stellt sich allerdings die Frage, wieso sie und ihr Geistesbruder ihre Zeit hier vertrödeln und nicht längst mindestens im Parlament, noch besser im "Koalitionsausschuss" sitzen. Da hält man sich auch nicht mit derlei "Kleinigkeiten" auf, und sie wären unter sich. Und wenn es wirklich jemand wagen sollte, der per Parlamentsbeschluss erzeugten Wahrheit "die Erde ist eine Scheibe" zu widersprechen, dafür sind ja dann die vorsorglich abgerichteten, durchgeknallten Sturmtruppen (samt johlender Staatsanwälte) zuständig. Sie haben es wirklich schon weit gebracht mit ihren selbst deklarierten Kleinigkeiten.

Und jetzt auch noch ein Ausflug in die Sprache der Diktatur. ER lässt wirklich nichts aus. Was "Kleinigkeiten" sind, bestimmt selbstverständlich ER, und nur ER, und das auch noch fallweise. Dann tauchen nicht existente "32"-er auf, weil ER sie hingeschrieben hat, für SEIN hochgestochen "Analyse" genanntes Geschwafel: Kleinigkeit. "Treffer" mit Tripelbedeutung: Kleinigkeit. X-fach nachgewiesene Logikfehler: alles Kleinigkeiten. Herbeiphantasierte Glocken, Mittelwerte, "Topperformance", Kleinigkeiten noch und nöcher. In irgendeinem SEINER Texte nicht auf derlei "Kleinigkeiten" zu stossen, erfordert vollständige Blindheit. Da sind Rechtschreibe- oder Rechenfehler wirklich die kleinsten "Kleinigkeiten", aber selbst diese weigert ER sich in SEINER bornierten Faulheit zu verbessern.