elementaar

Herrlich! Wie alles, was nur von Ferne nach einsichtiger Klugheit aussieht, bleibt es beim Forumschefignoranten, wie zu sehen, ohne Wirkung. Das ist aber nicht weiter schlimm. Lebbe geht weider.

Ist klar. ER gibt wieder den Otto. siehe auch: Pullover

Logische Unmöglichkeit. Sachs: Wahn! Wahn! Überall Wahn!

Die nächste lächerliche Falschaussage, wie üblich im Gewande des Dekrets. Falsch deshalb: Alles läßt sich mit Allem vergleichen: sowohl Äpfel mit Würstchen, wie auch Äpfel mit Birnen, wie auch Äpfel mit Würstchen und Birnen und Kernkraftwerken. Mit dem Kriterium "bequemste Art der Fortbewegung" fallen alle Viere durch. Es sind die Hohepriester und Jünger des Glaubens, die Vergleiche verbieten wollen, nicht die Wirklichkeitssucher. Lächerlich deshalb: ER behauptet doch die "Überlegenheit" SEINER Spielweise. Diese "Überlegenheit" soll sich doch gerade im Vergleich zum Zufallsgeschehen zeigen. Wie Jedermann weiß, wird sich diese "Überlegenheit" bei einem Pleinspiel mit Satzhöhenvariation in "Testspielen" niemals zeigen können. Wenn ER noch Hundert Jahre so weiter macht, käme ER auf 36.500 Sätze. Allermindestens müsste ER damit aber eine Umsatzrendite von durchgehend +66% erzielen. Daß dies nicht der Fall ist, hat das Turnier gezeigt. Watson: "Ich bin kein Idiot!" Sherlock: "Wie kommen Sie denn auf die Idee?"

Es wird natürlich rein gar nicht nützen: vor vielen Jahren zählte ich aus, wie viel Umsatz benötigt wird, wenn alle Fx bis zum Treffer Fx+1 verfolgt werden. In 37.000 Versuchen habe ich F2 bis F41 betrachtet. Lesebeispiel: Um den ersten F14 zu treffen, waren in dieser Stichprobe durchschnittlich 37,41 Stück aufzuwenden. Der längste Ausbleiber war in dieser Stichprobe der erste F38 mit 505 Stück oder 13,65 Rotationen.

Sag' ich ja. Also los: Einstellen des Aktenzeichens nicht vergessen.

Da ER ja, als Einziger!, hier immer den totalen Durchblick hat, bedeuten SEINE Aussagen also, daß der im Bundesanzeiger veröffentlichte Jahresabschluss zum Geschäftsjahr 2021 der Spielbank Wiesbaden nicht nur falsch ist, sondern sogar falsch sein muss. Glasklar! Da erwarte ich aber von IHM den sofortigen Gang zur Staatsanwaltschaft, um diese schändlichen Machenschaften sowohl der Spielbank, wie der Testatsprüfer zur Anzeige zu bringen. Soviel Bürgersinn muss man einfach von IHM einfordern. Statt daß ER SEINE und UNSERE Zeit damit verschwendet, UNS SEINE, wie immer, gänzlich überraschenden Erkenntnisse aufzunötigen. Hier hilft das gar nichts! Ab zur Staatsanwaltschaft! Nach erfolgter Anzeige bitte hier das Aktenzeichen einstellen, damit wir alle den Fortgang verfolgen können.

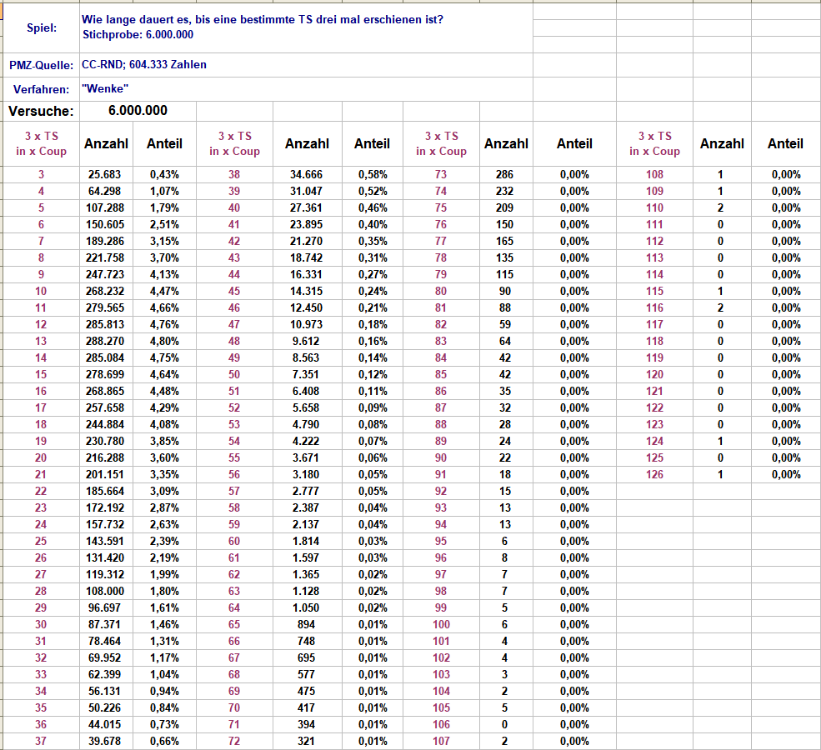
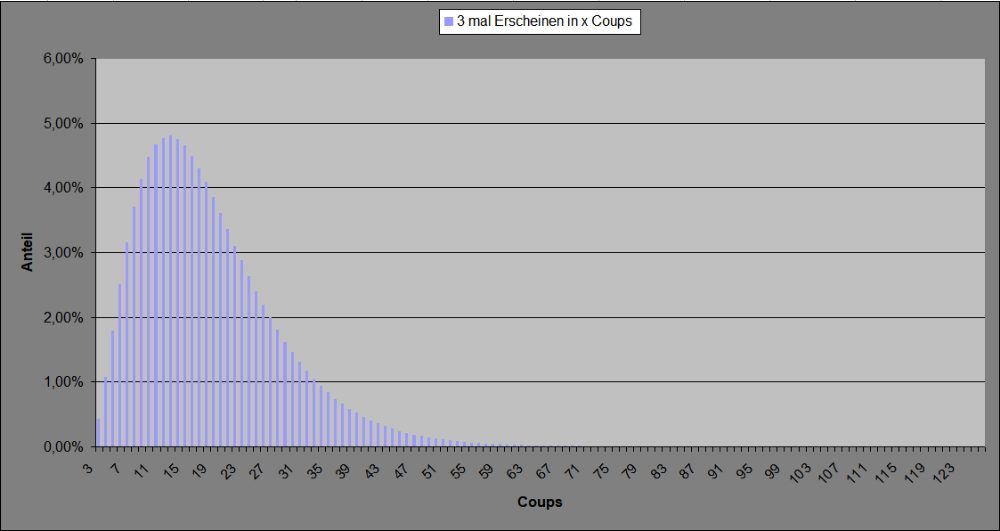
Bisher wurde nach der Erscheinenshäufigkeit auf einer begrenzten Coupstrecke gefragt. Möglicherweise erklärt sich die Beliebtheit derartiger Auszählungen mit dem relativ geringen Aufwand ihrer Erstellung und der Übersichtlichkeit der Ergebnisse, die die doppelte Begrenztheit mit sich bringt. In zwei mal 6 Coups kann eine bestimmte TS nur höchstens 12 mal erscheinen, mehr ist schlichtweg nicht möglich. Ganz anders ist die Lage, wenn man nach dem Coupverbrauch für eine bestimmte Erscheinenshäufigkeit fragt. Eine bestimmte TS kann beliebig lange ausbleiben. Möchte man den Coupverbrauch auszählen, hat man am langen Ende also eine offene Skala. Praktisch ist das erkennbar schlecht für ein systematisches Zählen. Wie viele Coups hintereinander muss ich anbieten, damit sich die geforderte Erscheinenshäufigkeit möglichst immer zeigen kann? Und damit zusammenhängend, wie ausladend muss die Zählskala sein? In der folgenden Auszählung wird nach dem Coupverbrauch für das dreimalige Erscheinen einer bestimmten TS gefragt. Die Beobachtungsstrecke habe ich auf 370 Coups begrenzt. Würde der Fall auftreten, daß diese Coupsstrecke für ein dreimaliges Erscheinen nicht genügte, würde dies unter ">370" gezählt, und wäre ein Ereignis mit < -8 sigma. In der Stichprobe von 6 Mio Versuchen hatte ich Glück, und der größte Coupverbrauch war lediglich 126 Coups (und damit etwas kleiner als -4 sigma). Abgebildet wird deshalb nur bis Coup 126, alle größeren Abstände wurden nullmal gezählt. Plausibilität: Dreimal dieselbe TS in drei Coups errechnet sich mit 6/37^3 = 0,004264308; bei 6.000.000 Versuchen sollte dies also 25.586 oder 0,43% mal der Fall sein. Der gezählte Wert stimmt gut überein. Mit 6,166666667 x 3 errechnet sich ein durchschnittlicher Coupverbrauch von 18,5 Coup. Alle 6 Mio Ereignisse produzieren einen Umsatz von 110.987.205 Stück und ergeben folglich einen Durchschnitt von 18,5 Coup. Die gezählten Werte stimmen mit 18,5 Coup gut überein. Ein Umsatz von 110.987.205 Stück sollte mit -2,70% ein Ergebnis von -2.999.654 Stück produzieren. Die gezählten Werte stimmen mit -2.987.205 und -2,69% gut überein und geben einen Hinweis in der zweiten Nachkommastelle, daß auch mit 6 Mio Versuchen die Schwankung an dieser Stelle noch nicht egalisiert wurde. Das Diagramm dieser Verteilung (anteilig): Ach herrje, ein solches Diagramm ist leider, aber sehr beruhigend, ein alter Bekannter. (Und jetzt bitte kein Ding-Dong-Gebimmel vom obersten Forum-Astigmatiker) Wir sehen ein steiles Ansteigen bis zum Scheitelpunkt in Coup 13, danach deutlich flacheres Absteigen bis es ab ca. Coup 37 so flach wird, daß man kaum noch etwas erkennen kann. Vielleicht doch noch mal die Wertetabelle, in etwas anderer Aufbereitung. Lesebeispiel und Bedeutungserläuterung: wie oben geschrieben, wurde der Coupverbrauch für dreimaliges Erscheinen einer bestimmten TS ermittelt. Damit in Coup 3 mit 0,43% aller Fälle eine TS zum dritten Mal erscheint, muß sie sowohl in Coup 1 wie in Coup 2 ebenfalls erschienen sein. Damit in Coup 6 mit 2,51% aller Fälle eine TS zum dritten Mal erscheint, muß sie in den Coups 1-5 zweimal erschienen sein. Ein Verlauf der Erscheinensabstände ist den Zahlen nicht zu entnehmen. Wir können also sicher sagen, bis Coup 18 werden wir in 57,73% aller Fälle ein dreimaliges Erscheinen einer bestimmten TS sehen, von Coup 19 bis 36 werden wir weitere 36,86% aller Fälle sehen. Über den Verlauf der Erscheinensabstände können wir (außer in Coup 3) jedoch keine sicheren Aussagen machen, dafür ist diese Auszählung nicht gemacht. Gruss elementaar PS: Ich muss mich für eine längere Weile verabschieden, andere Aufgaben verlangen meine Zeit und Aufmerksamkeit.

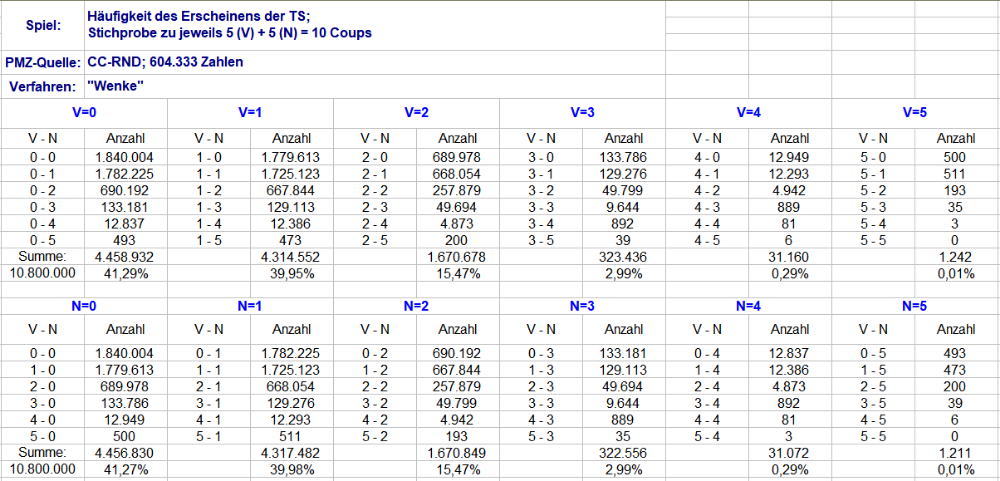
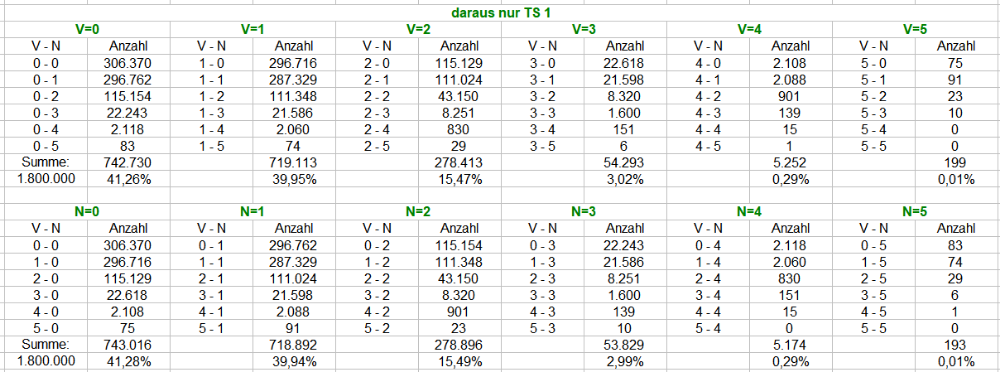
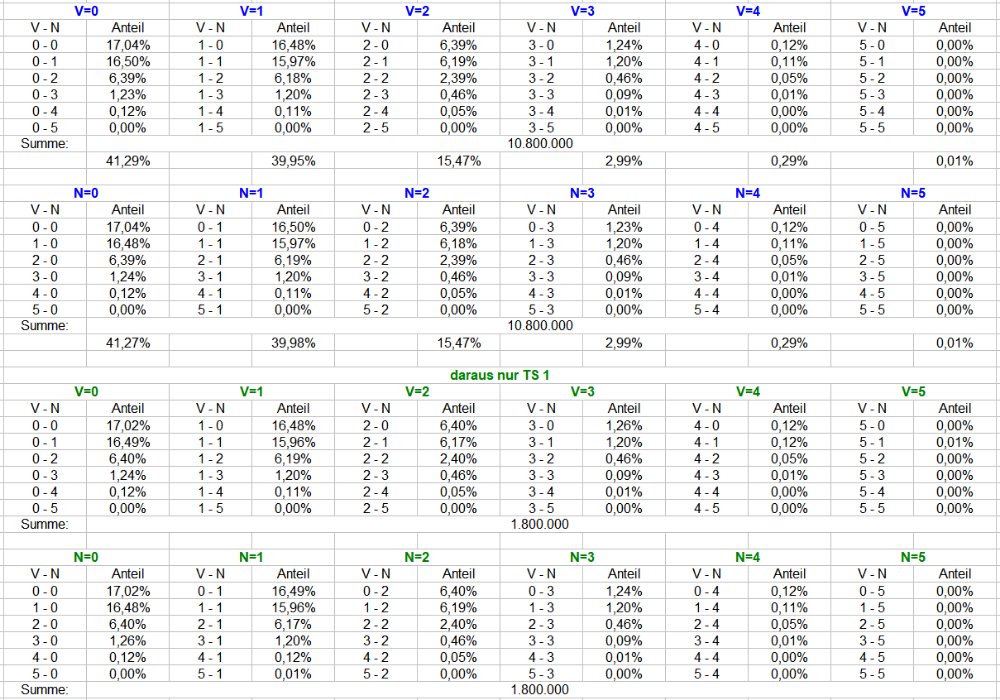
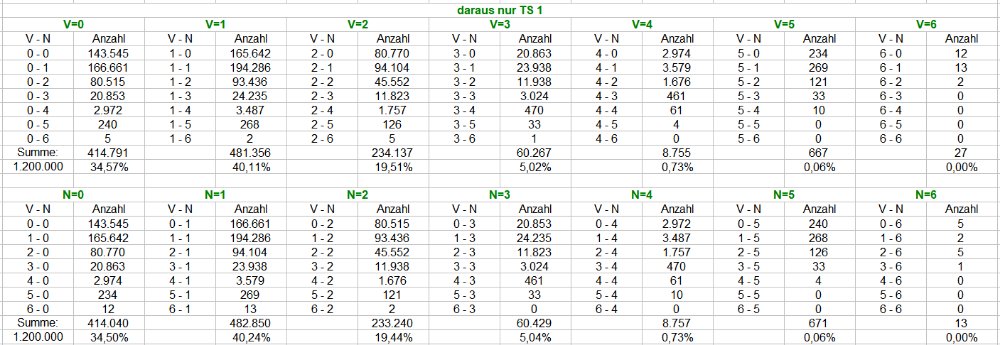
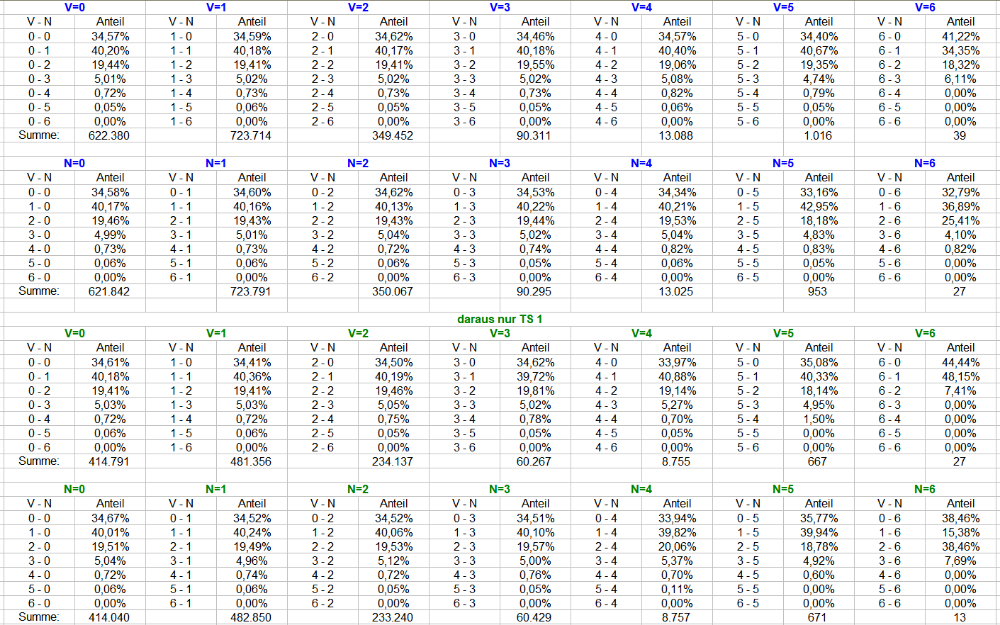
Die Auszählung mit jeweils 5 (V) + 5 (N) = 10 Coups. Die Gesamtanzahl beträgt 10,8 Mio Versuche. Das Späßchen mit TS1 habe ich beibehalten, weil sie ein Indiz der Schwankungsbreite beisteuert. TS 1 ist dabei ein Auszug aus denselben Permanenzen mit 1,8 Mio Ereignissen. Als Lesehilfe ist der Gesamtumfang jeweils blau markiert, TS 1 hingegen grün. Weitere Verständnishilfen bitte weiter oben nachlesen, der Aufbau der Tabellen ist analog. Der Tapetencharakter der Tabellen läßt sich ohne Zwischentexte leider kaum vermeiden. Gruss elementaar

Opd (Orator permanens diliramenti)

Hallo @Ropro, ob man unbedingt "sollte" weiß ich nicht, aber Glückwunsch zu dieser originellen Idee! Und natürlich hast Du recht: ein solch rollierendes Betrachten der Sechser-Pakete geben die Tabellen ohne weiteres her. Deiner Anregung, das mal mit Fünfer-Paketen zu versuchen, kann ich aber erst in ein paar Tagen nachkommen, da ich noch mit Folgen von TS-Erscheinensabständen beschäftigt bin. Gruss elementaar PS: In der anderen Frage: es hilft tatsächlich nur komplettes Ignorieren, mein "Stillhaltevorschlag" wurde abgelehnt, wie Du vielleicht gesehen hast.

Ganz toller Kalenderspruch, nur leider mal wieder falsch, weil unvollständig. Ein paar Gewissheiten gibt es sehr wohl beim Roulettespiel. Sie basieren alle (im Unterschied zu Vorgängen in Natur und Technik) auf der strikten Begrenzung der Grundgesamtheit: im Roulette mit den Zahlen 0-36 kann nur eine von 37 möglichen Zahlen im nächsten Coup erscheinen. Im nächsten Coup kann weder "Müllbeutel" noch "Eselskappe" herauskommen, nur eine von 37 vorher bekannten Zahlen. Etwas anderes ist unmöglich. Und weil das so ist, muß der erste F2 der Einzelzahlen mit spätestens 1 x 37 +1 Coups erschienen sein, ein "Ausreißer" darüber hinaus ist unmöglich muß der erste F3 der Einzelzahlen mit spätestens 2 x 37 +1 Coups erschienen sein etc. gibt es für jede endliche Coupstrecke eine vorher genau bestimmbare, abzählbare Anzahl aller möglichen Kombinationen, wie eine Permanenz überhaupt nur aussehen kann (und mit genügend Zeit auch wird). Und das alles Dank der strikten Begrenzung der Grundgesamtheit. Es könnte Leute geben, die sich diese Gewissheiten für ihr Spiel nutzbar gemacht haben. PS: Vorschlag: ER unterlässt das Traktieren "unseres" Themas mit SEINEN Anfällen von Fabulierlust, ich störe SEIN Thema nicht mit meinen Einsprüchen?

Hallo @Feuerstein, Dein letzter Beitrag war ja geradezu ein Wow!-Signal. Was Du da beschreibst, entspricht in weiten Teilen dem, wie ich auch vorgehe, und das im Gleichsatz mit allenfalls Überlagerung. Da ist Dir nun schon zum zweiten Mal nach https://www.roulette-forum.de/topic/23580-spiel-auf-dreier-figuren-mit-plus-progression/page/6/#comment-515365 ein Textstück gelungen, welches praktische Einsicht in einer Tiefe vermittelt, wie man es hier sehr selten antrifft. Da blieb mir, mit immer größer werdenden Augen und immer noch wachsender Zustimmung, zuweilen fast der Atem stehen. Dafür allerherzlichsten Dank! In dieser Dichte und Kürze, würde ich das selbst nicht hinbekommen haben; und wenn doch, hätte ich mich nicht getraut, es zu veröffentlichen. Deinen Mut und Deine Freigiebigkeit im Darstellen von Einsichten kann man nur bewundern. Obwohl ungerecht möchte ich aus meiner Sicht zwei besondere Perlen extra hervorheben: und Nochmals Dank, und für mich unzweifelhaft eine der Sternstunden dieses Forums. Gruss elementaar

Genau. Ich vermied diese Formulierung, damit ER uns in Ruhe lässt.

Als Grundmaxime ganz großartig! Für mich ist das die richtige Einstellung - und schön, sie auch in eher läppischem Zusammenhang, aber auch da zutreffend, zu lesen.

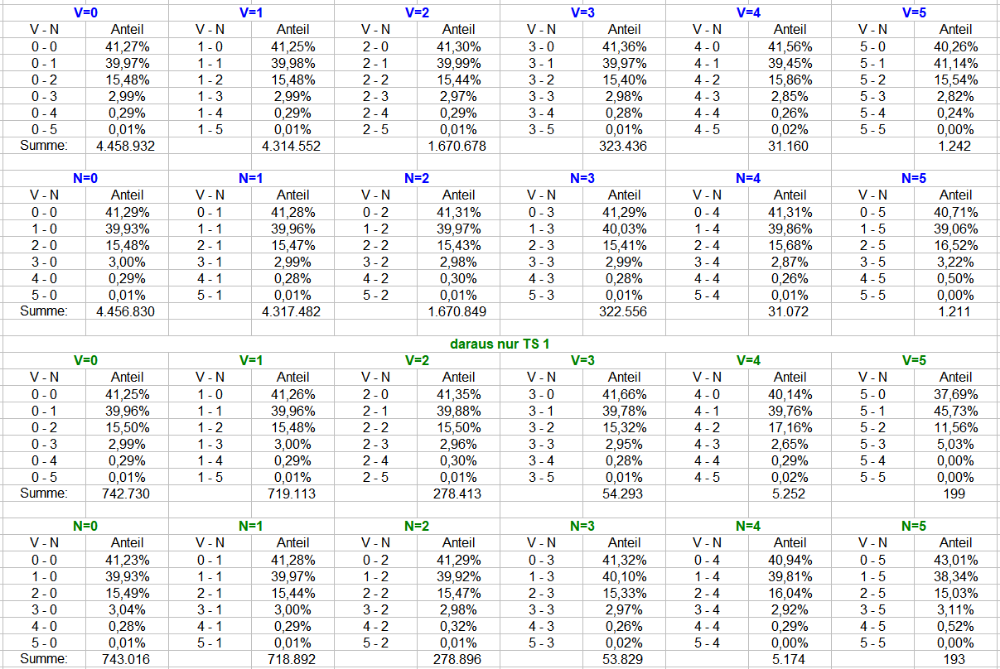
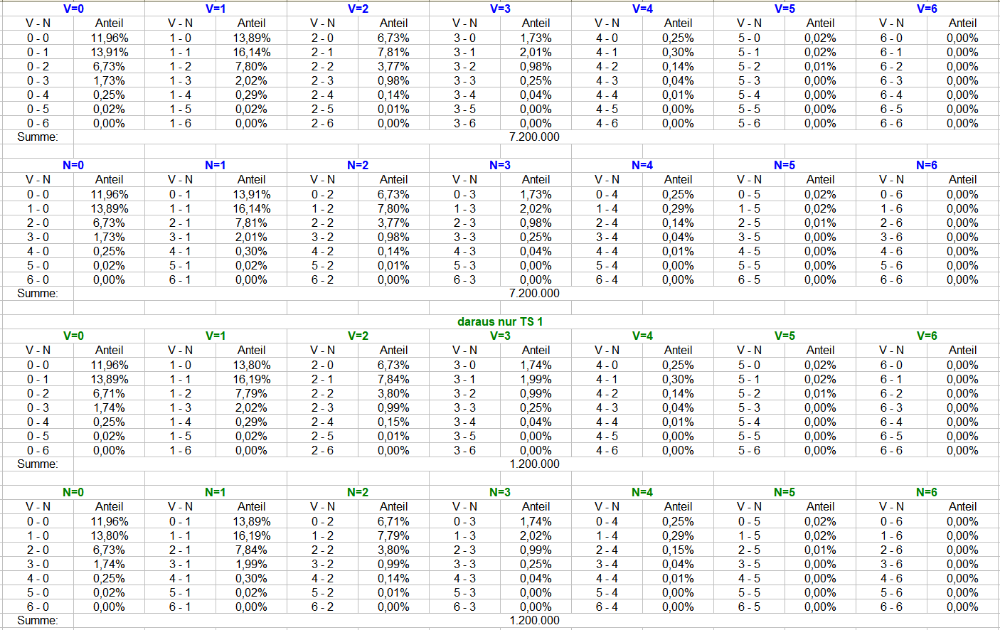
Die veröffentlichten Daten scheinen neuerlich von begrenztem Erkenntniswert zu sein (in wie weit das für Progressionen gilt, dazu mögen sich andere äußern - ich beziehe mich strikt auf Gleichsatz). Das ist aber weiter nicht verwunderlich, sondern vollkommen logisch: die Ergebnisse aus der (relativ) großen Zahl können gar keine Antworten für eine konkrete Spielsituation liefern - dazu wurden sie nicht erhoben. Falsche Frage an den falschen Datensatz sozusagen. Im praktischen Spiel befinden wir uns immer in einer konkreten Situation - was nach sehr langer Spielzeit herauskommt, ist für die gerade vorliegende Spielsituation nahezu unerheblich. Die große Zahl liefert lediglich den Hintergrund, verbunden mit der Mahnung, in ähnlichen Spielsituationen nicht immer dasselbe zu tun, denn was dann herauskommt, wissen wir, dank der großen Zahl. Betrachtet man die relativen Anteile, scheint die jeweilige Gleichwahrscheinlichkeit frustrierend und überwältigend, jedoch nur, wenn man mit den sowieso falschen Erwartungen an die Sache herangeht. Immerhin die "Neigung", daß in 6 Coups eine TS genau einmal erscheint, ist über alle Vorgänger und Nachfolger mit rund 40% am ausgeprägtesten, wobei kein Vorgänger aus sechs Coups irgendeinen sinnvollen Hinweis gibt, was in den nächsten sechs Coups zu tun sei. Betrachtet man die absoluten Anteile der Kombinationen, fällt dennoch etwas interessantes auf: Farblich markiert sind identische Erscheinenshäufigkeiten über 12 Coups. Lesebeispiel: 2-maliges Erscheinen einer bestimmten TS (blaßgrün) "0 - 2" mit 6,73%, "1 - 1" mit 16,14% und "0 - 2" mit 6,74% der Gesamterscheinungen. Beide "Konzentrationskombis" zusammen 6,73% + 6,74% = 13,47% sind damit < 16,14% der eher gleichmäßigen Verteilung. Eindeutig bevorzugt (= passiert häufiger) ist die eher gleichmäßige Verteilung über 12 Coups, gegenüber der Erscheinenskonzentration in nur jeweils sechs Coups. Das entspricht der Erwartung aus der Kombinatorik und ist als Tatsache banal. Gerade deswegen sollten wir es aber im Hinterkopf behalten - möglichst in beide Richtungen. Um im Beispiel zu bleiben: Es sei angestrebt in den nächsten 12 Coups eine bestimmte TS zweimalig zu treffen. Die ersten sechs Coups ergaben null Treffer. In dieser konkreten Spielsituation, weiß der Spieler aus den Tabellen: sein Spiel befindet sich in der 34,59%-Situation (absolute Anteile). sein Ziel von zwei Treffern wird er genau nur noch in 6,73% aller Fälle, und erweitert (zwei und mehr Treffer) in 8,74% aller Fälle erreichen (absolute Anteile). Innerhalb der erste-sechs-Coups-ohne-Treffer-Gruppe kann er sein Ziel genau mit 19,47%, erweitert zu 25,27% erreichen (relative Anteile). Bevor er nun weitere sechs Stück für die nächsten sechs Coups investiert, bieten sich, mindestens, diese Abwägungen an: wird sich die Permanenz in den nächsten sechs Coups eher gemäß der großen Zahl entwickeln? Wenn ja, dann kann er seine Erfolgswahrscheinlichkeiten wie gerade gezeigt ablesen, und sie ins Verhältnis mit dem Risiko (weitere sechs Stück) und der Gewinnhöhe (im besten Fall, zwei Treffer in den nächsten zwei Coups und Spielende bei +4) setzen. Wenn nein, dann benötigt er starke Argumente für ein Weiterspiel (oder Spielabbruch), die es durchaus geben kann, die aber in den obigen Tabellen mit Sicherheit nicht zu finden sind. In der Wirkung müssen seine Entscheidungen dazu führen, daß er sein Zwei-Treffer-Ziel deutlich häufiger als in 6,73% aller Fälle erreicht, so logisch wie trivial. Insgesamt bleibt festzuhalten: diese Art von Auszählungen sind nicht so konzipiert, daß sich aus ihnen ein eventuell darin verborgenes "Gewinngeheimnis" entschlüsseln ließe. Dafür werden sie nicht gemacht, und deshalb können sie folgerichtig auch keine Antwort auf eine solche Suche liefern. Gruss elementaar

Ursache und Wirkung unterliegen nicht per se dem Kommutativgesetz.

So ein KG setzt gemeinhin nach Abwurf (sonst ist er per Definition keiner; zuerst Kugelabwurf, dann G in K, dann Satz - so ist nun mal die Reihenfolge). Und jetzt mal scharf überlegen (am besten wie das Rattenschaf), ob das einen Unterschied machen könnte... Und wenn schon dabei, und falls intellektuell dazu in der Lage, wie man die entsprechenden wissenschaftlichen Untersuchungen mit Fabulierlust entkräften könnte.

Das sehe ich auch so, bloß anders formuliert. Zu der ersten Auszählung schrieb ich: Das hat sich mit der zweiten Auszählung und noch größerer Datenmenge bestätigt. (Die absoluten Zahlen sind größer als oben, weil ich nach der Veröffentlichung die Auszählung noch etwas weiter laufen ließ, um auch bei TS 1 auf die ursprünglichen 1,8 Mio Exemplare zu kommen.) Daneben deshalb die Anteilswerte. Haben wir in den ersten 6 Coups keinen Treffer erzielt, stehen also mit Saldo -6 in der Kreide, können wir nur in rund 25% der Fälle darauf vertrauen, daß wir "von selbst" und im Gleichsatz wieder mindestens auf Saldo "0" (oder darüber) kommen. Und nur hier, nämlich bei den >=2 Treffern würde ja progressiert. "Nur" deshalb, weil wir in rund 36% der Fälle auch nach den nächsten 6 Coups ohne Treffer dastehen werden, unser Saldo also -12 ist. Die Chance auf 12 Coups gar nicht zu treffen ist also immer noch größer, als mit Saldo -6 noch >=0 zu erzielen. Die Ursprungsidee von @Hans Dampf muß, meiner Ansicht nach, nicht weiter diskutiert werden. Spätestens das hier gezeigte Dreier-Trio mit Treffern genau im Erwartungswert, zeigte derart erschreckende Saldoverläufe, daß ich die mit Treffern unter Erwartungswert gar nicht sehen will. https://www.roulette-forum.de/topic/23580-spiel-auf-dreier-figuren-mit-plus-progression/page/6/#comment-515343 Eine Progression, die, mit Glück, im Grunde nur das wett macht, was sie zuvor selbst angerichtet hat, muß man, meiner Ansicht nach, keiner erweiterten Feinanalyse unterziehen. Das ist vielleicht vorschnell gedacht, aber, wie ganz oben schon einmal geschrieben: bei eigentlichen Progressionen fehlt mir die Kompetenz um sinnvoll mitdiskutieren zu können. Was man anhand der gelieferten Daten vertiefend betrachten könnte, dazu fällt mir schon einiges ein; es hat aber primär mit dem Progressionsthema nichts zu tun. Gruss elementaar

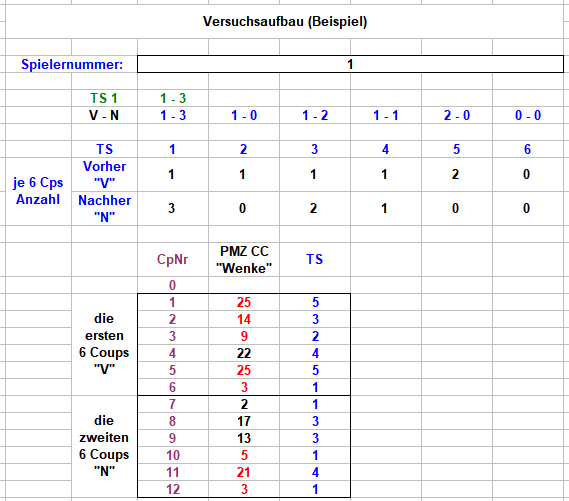
Womöglich unnötig, aber dennoch. Zur Verdeutlichung des Versuchsaufbaus zwei Bildschirmphotos als Beispiel. Spielernummer: Zum Beschleunigen des Auszählvorgangs richte ich mehrere Spieler parallel ein. Jeder Spieler erhält seine eigene, nur für ihn erzeugte Permanenz. Für das Beispiel ohne Belang. Spalte "PMZ CC "Wenke"": Für jeden Versuch wird eine neue Permanenz nach dem Verfahren "Wenke" erzeugt, hier jeweils 12 Coups lang. Die entsprechende TS ist in Spalte "TS" aufgeschlüsselt. Zeilen "je 6 Cps Anzahl": Hier werden die Vorkommen aller TS, also TS 1 bis TS 6 in der Permanenz getrennt nach "V" und "N" gezählt. Also bspw. TS 1: in den ersten 6 Coups 1 maliges Erscheinen, in den nächsten 6 Coups 3 maliges Erscheinen, als Kombination geschrieben "1 - 3" (in Zeile "V - N"); oder TS 5: in den ersten 6 Coups 2 maliges Erscheinen, in den nächsten 6 Coups 0 maliges Erscheinen, als Kombination geschrieben "2 - 0" (in Zeile "V - N") In Zeile "TS 1" (grün) wird dem Einzelauswertungswunsch von @Ropro entsprochen (es handelt sich also um einen spezifizierten Auszug aus der Gesamtmenge). Pro Versuch entstehen so 6 Kombinationen der 6 TS, die nachfolgend in der Zählliste hochgezählt werden. Von den 49 Kombinationen zeigt das Bild die ersten 21. In den fünf Spalten ganz rechts wird das Zählen mit den Ergebnissen von oben verdeutlicht, einmal (blau) für alle sechs TS in diesem Versuch, einmal (grün) für TS 1. Mit dem Übertrag der neuen Zählergebnisse in die Spalten "alle" und "TS 1" wäre dieser Versuch abgeschlossen. Der nächste Versuch startet mit dem Neuerzeugen einer weiteren Permanenz und analog. Das Verhalten einer bestimmten TS im zeitgleichen Verhältnis zu einer oder mehreren der anderen TS läßt sich mit dieser Art von Massenauszählung natürlich nicht studieren. Dafür müssten Verlaufsstudien angefertigt werden, die aber unvergleichlich aufwändiger sind. Gruss elementaar

Hallo @Ropro, vielen Dank für den Tabellenausschnitt zu Deiner Frage, das erleichtert die Antwort sehr. Es gilt immer, daß es sich bei Vorgänger und Nachfolger um exakt dieselbe TS handelt. Auch Vorgänger TS1 hat nur TS1 Nachfolger, und zwar immer in einer konkreten Permanenzsituation von jeweils 12 Coups betrachtet, sonst würde sie gar nicht in der Liste verzeichnet. Beim Text Deiner Frage könnte ein Typo unterlaufen sein: Der Zeilenabschnitt "3 - 2" bedeutet: TS1 kam drei mal in den ersten 6 Coups ("V") und zwei mal in den nächsten 6 Coups. Diese Kombi erschien in der Auszählung 11.938 mal Dieser Fall stünde bei "3 - 1" mit 23.938-maligem Erscheinen. Gruss elementaar

Aber gewiß doch. Dankeschön, Dir auch! Gruss elementaar

Hallo @Hans Dampf (von), Prima! Freut mich sehr. Du kannst vielleicht erahnen, wie erleichtert ich bin. Stimmt. An der Erscheinensanzahl selbst ändert sich nichts, nur die Wirkung. Gruss elementaar

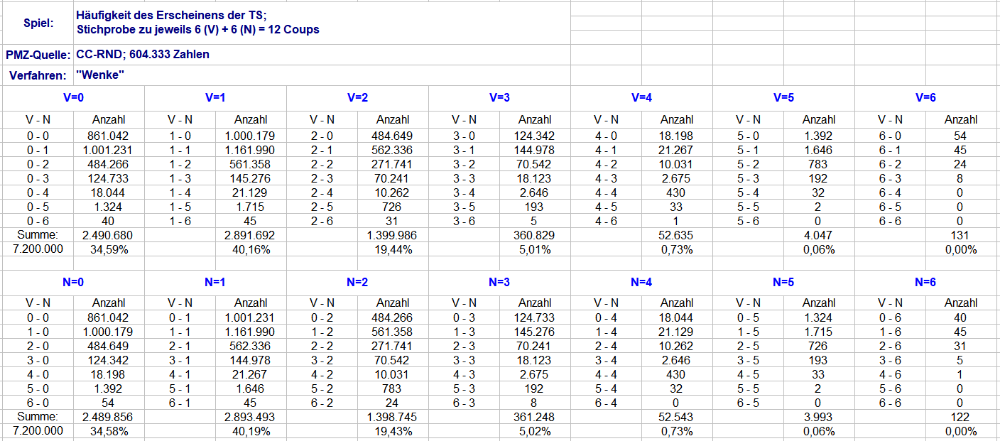
Hier kommt neuer, voll der Zahlenscheiß Mit neuen Permanenzen ergibt sich für alle TS nun eine Datenmenge von 7,2 Mio Versuchen. TS 1 ist dabei ein Auszug aus denselben Permanenzen mit 1,2 Mio Ereignissen. So kommen wir für eine einzelne TS wenigstens in die Nähe der oben angesammelten 1,8 Mio. Als Lesehilfe ist der Gesamtumfang jeweils blau markiert, TS 1 hingegen grün. Weitere Verständnishilfen bitte weiter oben nachlesen, der Aufbau der Tabellen ist analog. Gruss elementaar

Volle Zustimmung. Und immer wieder erstaunlich, mit wie wenig Zahlenmaterial man sich relativ viel Überblick verschaffen kann. Wie vielleicht schon verschiedentlich erwähnt, bin ich überhaupt kein Freund von riesigen Datenmassen, aber leider, wenn man sich auch für die Extreme interessiert, kommt man ab und zu nicht daran vorbei. Allein um sich aufs Neue persönlich davon zu überzeugen, daß das, was möglich ist, irgendwann auch tatsächlich Realität wird. Vor ein paar Tagen erst, beim Kramen in den alten TS-Unterlagen, stieß ich auf eine Datei, wo nach der Erscheinenshäufigkeit der TS gefragt wird. Aus Spaß ließ ich sie um eine weitere Portion Zahlen laufen und hatte danach das Ausbleiben einer einzelnen TS über 104 Coups in der Liste. Insgesamt waren dafür lediglich 1.2 Mio Versuche nötig. Rollierend im 6-Coup-Fenster ist es eine Übung in Demut, wenn man das erlebt. Aber das sind Ereignisse, die können und werden vorkommen, mit denen man als Spieler aber auch zurecht kommen muss.