elementaar
Mitglieder-
Gesamte Inhalte
988 -
Benutzer seit
-
Letzter Besuch
Inhaltstyp
Profile
Forum
Kalender
Articles
Alle erstellten Inhalte von elementaar
-
Spiel auf Dreier-Figuren mit Plus-Progression
topic antwortete auf elementaar's mamarketing in: Einfache Chancen
Ausgesprochen viel. Meiner Meinung nach kann deren Bedeutung gar nicht überschätzt werden. Es ist ein Mittel der Entwicklung einer Permanenz auf die Spur zu kommen (zumindest in der Einbildung und in lichten Momenten). Wenn mich etwas wirklich interessiert, dann programmiere ich mir so eine Art automatisch ablaufendes Mäusekino der Permanenzentwicklung und studiere das bewegte Treiben. Zumindest mir hat das zu einigen wichtigen Einsichten verholfen. Da ist man wirklich hart am Ball. Für statische Massenauszählungen benutze ich sie nicht mehr, weil man sowieso so viele Ereignisse braucht, daß sich die rollierend gewonnenen in der Datenmasse auflösen (müssen). -
Spiel auf Dreier-Figuren mit Plus-Progression
topic antwortete auf elementaar's mamarketing in: Einfache Chancen
Hallo @Hans Dampf (von), leider weiß ich so langsam nicht mehr, wie ich es Dir erklären könnte. Fangen wir mal mit dem Nullstellen des Saldos an. Wenn ich viel weiter oben schreibe "Stichprobe von 30 mal 111 Coups", dann ist genau das, was geschrieben steht, auch gemeint und hat tatsächlich, real, so stattgefunden. Es fanden 30 Versuche statt. Versuch Nummer 1: Partiestart bei Coup 1, Partieende (und tatsächlich ENDE) bei Coups 111. Dazwischen wird gezählt, was einen gerade interessiert, Erscheinenshäufigkeiten, Saldostände, Punkte, die man explizit betrachten will etc. Danach werden die Befunde in eine gesonderte Liste eingetragen. ENDE von Versuch Nummer 1! Danach beginnt Versuch Nummer 2 mit exakt denselben Bedingungen wie Versuch Nummer 1, nur mit einer anderen Permanenz. Und wenn man sich für Saldostände und "0"-Schneidungen interessiert, fängt jeder einzelne Versuch selbstverständlich wieder mit Saldo "0" an. Was denn sonst? Es findet weder ein Saldoübertrag (was Dir vielleicht, dann aber irrtümlich, vor Augen steht) noch sonst irgendwas statt, was Bezug auf Versuch Nummer 1 hätte. Jeder Versuch ist voneinander vollständig unabhängig und deshalb unmittelbar vergleichbar. Vielleicht hilft, wenn Du Dir für jeden einzelnen Versuch einen anderen Spieler vorstellst. Alle Spieler (=Anzahl der Versuche) starten mit Saldo Null, solange sie noch nichts gesetzt haben. Hat man bei TS mit Erwartungswert -2,7% 6 x 37 = 222 Coups gesetzt, hat man durchschnittlich 6 Stücke Minus erzielt. Um von denen auf Saldo Null zu kommen, muß man einen Treffer über dem Erwartungswert der Chancengröße haben. Hat man erst 1 x 37 Coups gesetzt, hat man durchschnittlich 1/6-Stück (der Chancengröße) Minus erzielt. 1/6 ist kleiner als 1, entsprechend häufiger wird man eine "0"-Schneidung sehen, weil man weniger Treffer über Erwartungswert haben muß. Ja natürlich. Nur ist das beim Zählen von "0"-Schneidungen unerheblich. Da ist entscheidend, wie lange (für welche Coupsstrecke) gezählt werden soll. Es findet beim Verkürzen der Betrachtungsstrecke kein Saldoübertrag statt. Das wäre ja absurd. Heißt es, ich soll Partien mit 25 Coups auszählen, dann mache ich das, und fange jede einzelne Partie selbstverständlich mit Saldo Null an. Etwas anderes kommt (aus wirklich sehr vielen Gründen) gar nicht in Frage. Heißt es, ich soll Partien mit 25 Coups bis zu einer Gesamtstrecke von 100 betrachteten Coups auszählen, dann ergibt das 4 Partien, die alle vier mit Saldo Null starten. Und das ist etwas anderes, als wenn ich 1 Partie mit 100 Coups auszähle. Nicht nur wegen des unwahrscheinlicher Werdens von Saldo-"0"-Schneidungen mit steigender Betrachtungsdauer, sondern auch, weil das Anteilsverhältnis von Coup 1, in dem es keine Saldo-"0"-Schneidung geben kann, bei unterschiedlichen Betrachtungsstrecken eben unterschiedlich ist. Gruss elementaar -
Spiel auf Dreier-Figuren mit Plus-Progression
topic antwortete auf elementaar's mamarketing in: Einfache Chancen
Wird gemacht. Die Schwankungen werden bei bloß 300 Tsd Ereignissen natürlich in allen Kombinationen größer sein. Ich schaue mal, auf wie viele ich darüber hinaus komme. -
Spiel auf Dreier-Figuren mit Plus-Progression
topic antwortete auf elementaar's mamarketing in: Einfache Chancen
Ernsthaft? Das könnte ich morgen erledigen, die Routine ist ja eingerichtet. Welche TS soll's denn sein? -
Spiel auf Dreier-Figuren mit Plus-Progression
topic antwortete auf elementaar's mamarketing in: Einfache Chancen
Hallo @Feuerstein, freut mich sehr, wenn es auf Dich so wirkt. Das ist geradezu der erhoffte Idealfall. Danke! elementaar -
Spiel auf Dreier-Figuren mit Plus-Progression
topic antwortete auf elementaar's mamarketing in: Einfache Chancen
Hallo @Hans Dampf (von), Da rate ich aber dringend, diese Aussage noch einmal zu überdenken. Zu jedem Anfang einer Betrachtung, sozusagen in Coup 0, steht auch die Saldokurve bei Null. Es wurde noch nichts gesetzt, es wurde weder verloren noch gewonnen. Mit Coup 1, egal welche der 6 TS gesetzt wurde, ist der Saldo entweder -1 oder +5, erschien Zéro steht der Saldo bei allen sechs möglichen TS bei -1, sonst fünf TS mit -1, und eine, die Treffende, mit +5. Mehr geht nicht nach Coup 1. Und selbstverständlich ist es da ein Unterschied, ganz real und von mir aus auch mit Geld unterlegt, ob ich für 100 Coups Gesamtspielzeit den Saldo vier mal wieder auf Null stelle, oder einmal durchspiele, ganz wie oben vorgerechnet. Gruss elementaar -
Spiel auf Dreier-Figuren mit Plus-Progression
topic antwortete auf elementaar's mamarketing in: Einfache Chancen
Hallo @Ropro, Ja ganz richtig. Das Wichtigste dabei ist aber, daß es ohne die dazugehörigen "N" keinen Eintrag gibt. So ist zwangsweise sichergestellt, daß zu jeder "V" TS nur der Nachfolger derselben TS verzeichnet wird. Real habe ich also alle 49 möglichen Kombinationen ausgezählt. Um im Beispiel zu bleiben: im Vorlauf und zwangsweise Nachlauf so würde bei "0 - 3", "0 - 2", "0 - 1" jeweils um 1 hochgezählt. Durch die auch in dieser Auswertung wieder bestätigte Gleichwahrscheinlichkeit, würden sich die Befunde nicht ändern, man müsste nur das sechsfache an Zeit aufwenden, um auf 1,8 Mio Versuche zu kommen Gruss elementaar -
Spiel auf Dreier-Figuren mit Plus-Progression
topic antwortete auf elementaar's mamarketing in: Einfache Chancen
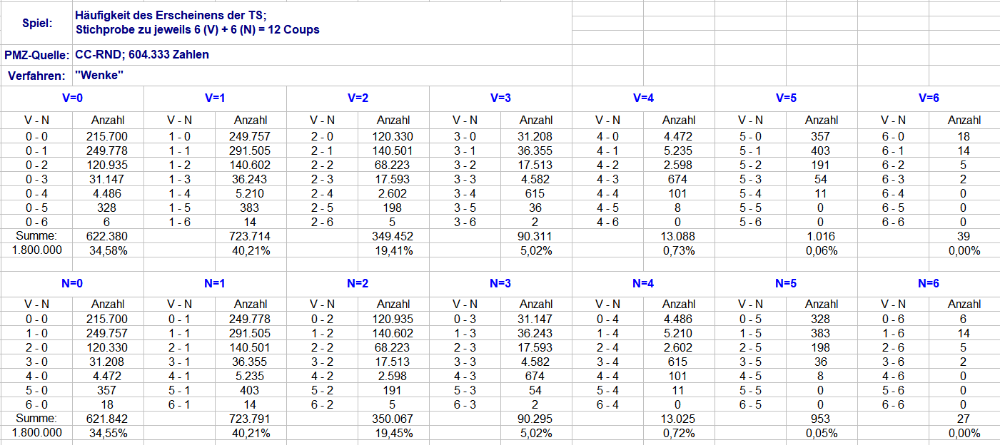
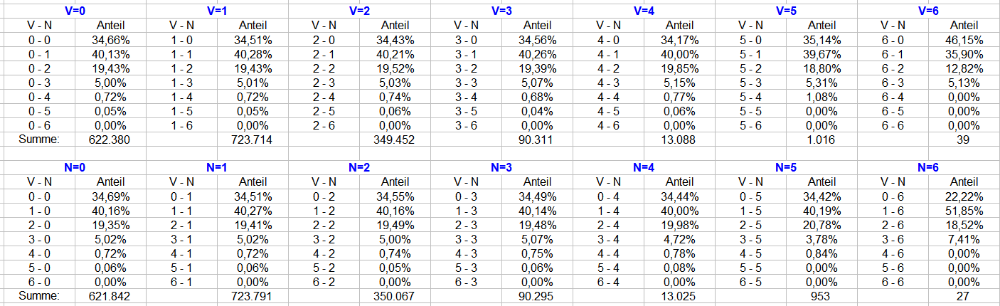
Versuchsaufbau: In 6 Coups wurde das Erscheinen der TS gezählt ("Vorher"). In den unmittelbar darauffolgenden 6 Cps wurde das Erscheinen derselben TS gezählt ("Nachher"). Dies habe ich insgesamt 1,8 Mio mal ermitteln lassen. Die Ergebnisse weiter unten. Die Gründe für die kurzen Vorgänger/Nachfolger-Paare erläutert: 6 Coups ist die (abgerundet) kleinste diskrete Zahl, die man als TS-Rotation begreifen kann. In 6 Coups kann eine TS 0 bis 6 mal erscheinen. Vorgänger/Nachfolger bilden also 7 x 7 = 49 mögliche Kombinationen. Diese 49 Kombinationen kann man ebenfalls als eine Art "Rotation" auffassen. Mit 1.800.000 / 49 habe ich also rund 36.735 dieser gedachten Rotationen verarbeitet. Eine längere Betrachtungsstrecke läßt die Zahl der benötigten Versuche explodieren, bspw. 37 Coups + 37 Coups ergibt 38 x 38 = 1.444 Kombinationen, 50 Coups + 50 Coups ergibt 51 x 51 = 2.601 Kombinationen. Für 36.735 dieser "Rotationen" würde ich also allermindestens 53.045.340 bzw. 95.547.735 Versuche benötigen. Zeitlich ist das für mich nicht zu leisten. Zumal die Auszählung auf kürzest sinnvolle Strecke den Vorteil des einfachen Kopfrechnens bietet. Definition der Abkürzungen: "V" = "Vorher" = die ersten sechs Coups = die Coups mit der laufenden Nummer 1 bis 6 "N" = "Nachher" = die zweiten sechs Coups = die Coups mit der laufenden Nummer 7 bis 12 "=Zahl" = Anzahl des Erscheinens einer bestimmten TS innerhalb von sechs Coups. "V=0" bedeutet also: in den ersten sechs Coups ist eine bestimmte TS null mal, also gar nicht, erschienen; "N=3" bedeutet, die in "V" betrachtete TS ist in den zweiten sechs Coups drei mal erschienen. Kurzschreibweise "1 - 0" bedeutet: eine bestimmte TS ist in den ersten sechs Coups ein mal erschienen, dieselbe TS ist in den zweiten sechs Coups null mal erschienen. Zunächst die absoluten Zahlen: Lesebeispiel: ist eine bestimmte TS in den ersten 6 Coups einmal erschienen, erschien dieselbe TS in den nächsten 6 Coups 5.210 mal viermal ("1 - 4"). Plausibilität: Die Anzahl der gefundenen Erscheinenshäufigkeiten sollten bei "Vorher" und "Nachher" ungefähr gleich sein. Das ist hier gegeben. Wie immer gilt: je kleiner die Anzahl der gefundenen Kombination, desto unsicherer (schwankungsstärker) ist das Ergebnis. Auf die paar Exemplare für sechsmaliges Erscheinen, sowohl "Vorher" wie "Nachher" wird wohl niemand eine Strategie aufbauen wollen. Die relativen Werte pro Abteilung (also nicht bezogen auf die gesamten 1,8 Mio) Was kann man damit nun anfangen? Zunächst wird eindrücklich dokumentiert, wie gleichwahrscheinlich die Erscheinenshäufigkeit auch in unmittelbarer Vorgänger/Nachfolger-Betrachtung auf 6 Coups ist. Erblickt man in den ersten 6 Coups eine TS null mal, wird man auch in den nächsten 6 Coups diese TS zu 34,66% null mal sehen. Ungefähr denselben Anteil erhalten wir aber auch mit V=1 bis V=4 (danach sind es zu wenige Ereignisse). Aber darum geht es bei der Rücklauffrage ja nicht. Zur Beantwortung dieser Frage ist tatsächlich mal ein wenig Rechnen erforderlich. Für 6 Coups bedeutet: 0 mal Erscheinen = Saldo -6 1 mal Erscheinen = Saldo 0 2 mal Erscheinen = Saldo +6 3 mal Erscheinen = Saldo +12 4 mal Erscheinen = Saldo +18 5 mal Erscheinen = Saldo +24 6 mal Erscheinen = Saldo +30 1 mal Erscheinen = Saldo 0 ist einfach. Sowohl Vorgänger wie Nachfolger (1 - 1) kehren innerhalb von 6 Coups zur Null zurück. Ob von oben (Plussaldo) oder von unten (Minussaldo) kann mit dieser Auswertung nicht festgestellt werden. 0 mal Erscheinen = Saldo -6 bedeutet, daß der Nachfolger 2 oder mehr Erscheinen benötigt, damit die Null-Linie mindestens einmal von unten geschnitten wird. Das ist 156.902 mal oder 25,21% (aller V=0-Fälle) der Fall. 2 bis 6 maliges Erscheinen in den ersten 6 Coups bedeutet einen Plussaldo (maximal einmaliges Schneiden der Null-Linie), der jedoch nur bei V=2 und beim Nachfolger N=0 die Null-Linie von oben schneiden kann. Alle anderen Vorgänger bleiben bei egal welchem Nachfolger über der Null-Linie. Zum Schluss kann man sich natürlich auch dafür interessieren, wie sich der Anteil der Kombinationen am Gesamtgeschehen (1,8 Mio Versuche) darstellt. In den Tabellen sind sehr viele Daten enthalten, ich weiß. Ein gründliches und verständiges Studium ist unumgänglich; das erfordert aber Zeit und Arbeit. Man attackiere bitte nicht den Boten. Gruss elementaar -
Spiel auf Dreier-Figuren mit Plus-Progression
topic antwortete auf elementaar's mamarketing in: Einfache Chancen
-
Spiel auf Dreier-Figuren mit Plus-Progression
topic antwortete auf elementaar's mamarketing in: Einfache Chancen
Dieser Unterschied besteht in Hinblick auf die "0"-Schneidungen. In Coup 1 kann es bspw. keine Schneidung geben. Anteil auf 100 Coup = 1/100; Anteil auf 25 Coups = 4 x 1/25. Umgekehrt wird der Anteil an "0"-Schneidungen bei Verlängerung der Betrachtungsstrecke immer geringer werden, weil sich alle TS dem Erwartungswert nähern. Mit -2,7% wird ein erneutes Schneiden der "0"-Linie immer unwahrscheinlicher. Deshalb, weiter oben, meine Frage nach der Länge der Betrachtungsstrecke. Falls man "0"-Schneidungen praktisch nutzen wollte, müsste man erst einmal die optimale Betrachtungsstrecke für Saldo "0" herausfinden (mit welcher Coupstrecke sind relativ die "meisten" Saldo-"0"-Schneidungen zu erwarten?) Falls man "0"-Schneidungen praktisch nutzen wollte, und sie relativ unabhängig vom Coupverbrauch sein sollen, dann müsste man die relative "0"-Linie des Erwartungswertes (-2,7%) benutzen, das wäre dann eine Gerade, die mit -2,7% vom Umsatz absteigt. Gruss elementaar -
Spiel auf Dreier-Figuren mit Plus-Progression
topic antwortete auf elementaar's mamarketing in: Einfache Chancen
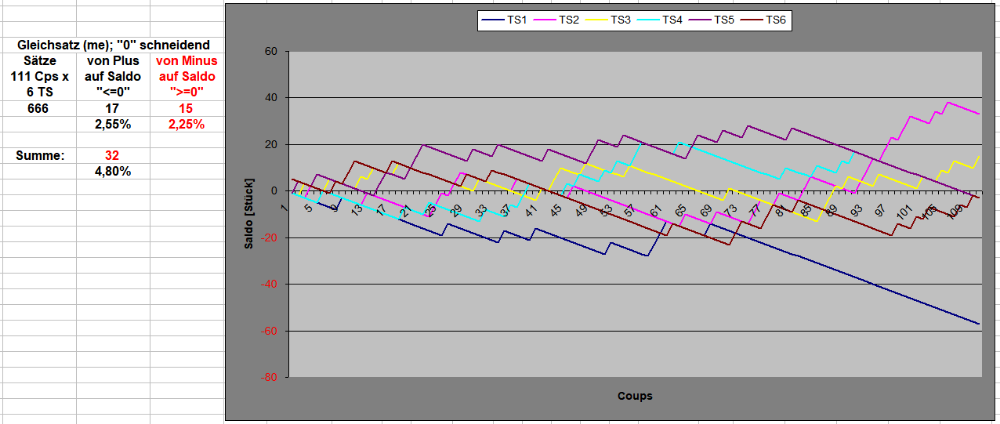
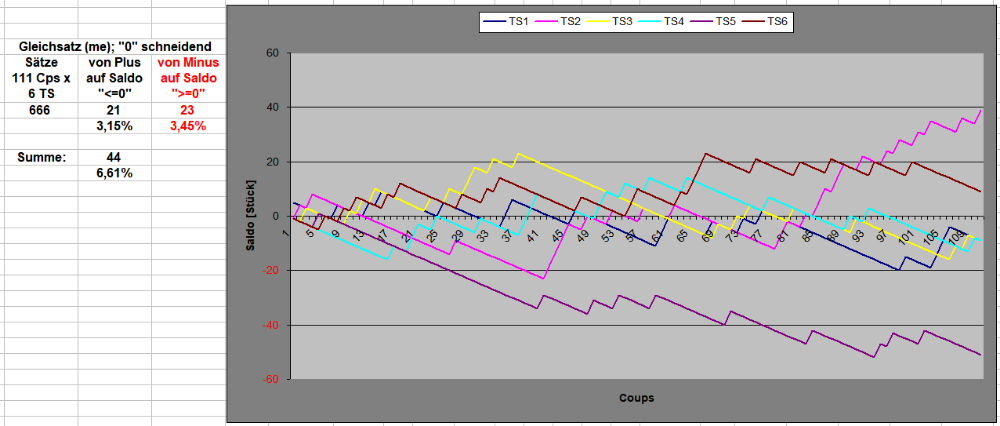
Hallo @Hans Dampf (von), Die kann man durchaus herstellen, jeweils für einen Versuch über 111 Coups. Wollte ich das für eine einzelne TS machen, wäre ich allerdings bis zum Sankt-Nimmerleins-Tag beschäftigt, und @Paroli würde mir vielleicht auf's Dach steigen, weil ich seinen Serverplatz mit Bildchen zupflastere. Deshalb alle sechs zeitgleichen TS in einer Graphik und, wie oben, mit drei unterschiedlichen Szenarien. Beispiel für unterdurchschnittliche Anzahl an "0"-Schneidungen von 6 TS in 111 Coups Beispiel für durchschnittliche Anzahl an "0"-Schneidungen 6 TS in 111 Coups Beispiel für überdurchschnittliche Anzahl an "0"-Schneidungen 6 TS in 111 Coups Der erste Eindruck mag vielleicht der einer gewissen Unübersichtlichkeit sein, man kann jedoch sehr schön studieren, wie sich eine (oder mehrere) TS im Verhältnis zu den anderen bewegen. Gruss elementaar -
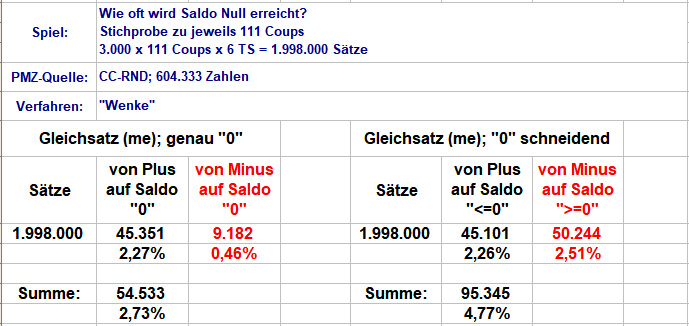
Spiel auf Dreier-Figuren mit Plus-Progression
topic antwortete auf elementaar's mamarketing in: Einfache Chancen
Zur Matrix muß ich noch Text schreiben, das wird morgen geschehen. Zum Unterschied von "genau 0" und "0 schneidend": Es gibt fünfmal mehr Nichttreffer als Treffer. Bei "genau 0" muß der Saldo vor Treffer genau -5 betragen, sonst landet man bei Treffer nicht auf "genau 0". Gruss elementaar -
Spiel auf Dreier-Figuren mit Plus-Progression
topic antwortete auf elementaar's mamarketing in: Einfache Chancen
Hallo @Hans Dampf (von), Du raubst einem aber wirklich jede Illusion. Da war ich so froh, endlich mal eine klare und eindeutige Antwort ohne Interpretationsspielraum geben zu können, da kommst Du mit Deiner Präzisierung um die Ecke - sei's drum, so eine Ahnung in die Richtung hatte ich schon... Ähnlich wie @Feuerstein, dessen Einsichten zur Progressionsvorbereitung und -gestaltung ich ganz besondere Beachtung wünsche, habe ich auch in die Tiefen meiner Festplatten geschaut, und leider nicht wiedergefunden, an was ich mich erinnere. Um das Thema "Rücklauf" besser darstellen zu können, erstelle ich nun neu eine Vorher-Nachher-Matrix (für andere Chancengrößen wiedergefunden, für TS leider nicht). Vor übertriebenen Erwartungen an die Ergebnisse möchte ich aber schon mal vorsorglich warnen. Gruss elementaar -
Spiel auf Dreier-Figuren mit Plus-Progression
topic antwortete auf elementaar's mamarketing in: Einfache Chancen
Fett im Zitat von mir. Falls Du wirklich wörtlich meinst, was Du schreibst, ist die Antwort so eindeutig wie einfach: nie (wenn wir Zérokapriolen außen vor lassen). Weil 100 Coups kein Vielfaches der Auszahlung "6" für TS ist. Gruss elementaar -
Spiel auf Dreier-Figuren mit Plus-Progression
topic antwortete auf elementaar's mamarketing in: Einfache Chancen
Selbstverständlich. Deshalb haben die landläufigen Massenuntersuchungen auch nur einen sehr begrenzten Erkenntniswert, weil sie konkretes Permanenzgeschehen nicht genügend genau spiegeln, und zwangsläufig auf Durchschnittswerte hinauslaufen. Mit Deiner Frage sind wir dann aber bei Spieltechnik und -taktik. Auf Dauer (unendlich) und "von alleine" bringen sowohl a) wie b) keinerlei Vorteil. Ganz anders sieht es auf begrenzter Spielstrecke aus. In Phasen wo überwiegend nicht oder zu spät getroffen wird, ist a) das Mittel der Wahl (wobei ich dann lieber etwas anderes spiele und den Verlaufsgraphen nur beobachte, bis sich wieder etwas interessantes in ihm regt). In Phasen wo überwiegend schnell und gut getroffen wird, ist b) angezeigt, mit beherzter Satzhöhensteigerung, wenn man möchte. Schlimm wird es allerdings, wenn keine der beiden Phasen vorliegen. Auch dafür muß man eine Lösung finden, oder konsequent nicht setzen. So formuliert sind das allerdings Banalitäten, die auch Opa hinter dem Ofen vor sich hin murmeln könnte, aber wer weiß? Vielleicht hilft's jemandem. Gruss elementaar -
Spiel auf Dreier-Figuren mit Plus-Progression
topic antwortete auf elementaar's mamarketing in: Einfache Chancen
Neufelius (die website gibt es scheinbar nicht mehr) hat den absoluten Ausgleich per Auszählung untersucht. Da mir seine Datenbasis etwas zu mager erschien, habe ich seine Versuchsanordnung nachvollzogen und kann seine Befunde bestätigen. Grob gesagt: der absolute Ausgleich kommt entweder sehr schnell oder eher gar nicht. Macht man sich klar, daß jede Permanenz eine Figur der Kombinatorik ist, leuchtet das auch unmittelbar ein: die Figuren mit absolutem Ausgleich werden mit steigender Coupszahl relativ seltener (EC ohne Zéro: 2er Figur: 50%; 4er Figur: 37,5%; 6er Figur: 31,25% etc.) Gruss elementaar PS: Wie vertrackt das mit der Betrachtungszeit sein kann, mag folgendes Beispiel illustrieren. Angenommen wir spielen eine EC 6er Figur (könnte auch Progressionssequenz sein), und fahren in den ersten drei Coups drei Minus ein, dann verhilft uns innerhalb der 6er Figur nur noch eine einzige Kombination (1/64=1,56%) zum Ausgleich; andererseits stehen die Chancen in den nächsten drei Coups die eine, genau richtige 3er Figur zu treffen 1/8=12,5%. -
Spiel auf Dreier-Figuren mit Plus-Progression
topic antwortete auf elementaar's mamarketing in: Einfache Chancen
Hallo @Hans Dampf (von), Und schon stecken wir im uferlosen Schlamassel. In welcher Zeit (Coupverbrauch) soll dieser Rücklauf betrachtet werden? Ist mit "Null" Saldonull gemeint oder lediglich ein Treffererscheinen gemäß des Erwartungswertes? Es ist ja klar, daß, mit längerer Betrachtungsstrecke ein Saldonull immer unwahrscheinlicher wird, weil dazu überdurchschnittlich viele Treffer benötigt würden, man müsste also über Erwartungswert treffen (oder die Satzhöhe soll es richten). Ist jedoch ein relativer Rücklauf gemeint, bekommt die Zeit (Coupverbrauch) eine weitere Bedeutung, weil sie allein schon in der Lage ist, einen relativen Ausgleich herbeizuführen, ohne daß die absolute Trefferzahl zur "Null" führt. Deine vernünftigen Fragen lassen sich ohne das Postulieren von Zusatzkriterien nicht klar beantworten - und findet man eine klare Antwort, gilt sie nur für die zuvor definierten Spezialfälle. Das kann man Dilemma nennen. Gruss elementaar -
Spiel auf Dreier-Figuren mit Plus-Progression
topic antwortete auf elementaar's mamarketing in: Einfache Chancen
Hallo @Hans Dampf (von), Von diesen 58% werden leider die meisten Exemplare als "Indikator"-Sequenzen nach Nichttrefferstrecken >5 verbraucht. Das ist gut und im Sinne des Spielaufbaus, wenn sich die Nichttrefferstrecken >5 zu Serien ballen (0,42 x 0,42 x etc.). Das ist schlecht, wenn sich die Trefferstrecken <=5 nicht genügend lange ballen, oder wenn sich Nichttrefferstrecken >5 mit Trefferstrecken <=5 einfach abwechseln (0,42 x 0,58 x 0,42 x 0,58 etc.). Die "Indikator"-Sequenz räumt mit derselben Satzhöhe bloß ein paar Minusstücke der jüngst vergangenen Nichttrefferstrecke >5 ab. Erst danach könnte mit der jetzt erhöhten Satzhöhe etwas getilgt werden. Nach jeder Nichttrefferstrecke >5 benötigen wir also mindestens eine Zweierserie der Trefferstrecke <=5 (0,58 x 0,58). Die ist zwar immer noch häufiger als eine Nichttrefferserie >5, aber doch deutlich seltener als es die 58% suggerieren könnten. Mit diesen 58% gewinnen wir durchschnittlich 1,962183 Stück, die 42% dagegen produzieren jedoch durchschnittlich -2,124850 Stück; die Trefferstrecken <=5 würden also möglichst vollständig gebraucht. Um bloß den Hausvorteil wett zu machen, müsste jede einzelne von ihnen mindestens durchschnittlich 0,162667 Stück gut machen. Das alles weißt Du wahrscheinlich schon längst, insofern sind wir bei den Eulen. Sehr interessant fand ich dennoch, was die Progression bei Trefferlagen genau im Erwartungswert anrichtet, und wie sie es tut. Die Diagramme dazu sind für mich ein Lehrbeispiel und Mahnmal, wie gefährlich selbst die Seitwärtsbewegungen wirklich sind. Im praktischen Spiel ist man ja nur zu gern bereit, sich mit dem Spruch "zumindest nicht (hoch) verloren" zu trösten. Basiert das Spiel auf keinem positiven Erwartungswert, ist das Augenwischerei: die "Umsatzschuld" hat sich in den Kulissen längst aufgebaut. Gruss elementaar -
Spiel auf Dreier-Figuren mit Plus-Progression
topic antwortete auf elementaar's mamarketing in: Einfache Chancen
Hallo @Feuerstein, So könnte man es zusammenfassen. Was mich aber wirklich freut, ist, daß es uns gelungen ist zu demonstrieren, daß man sich auch auf zivilisierte Art über ein Roulettethema unterhalten kann. Für mich ein Wert an sich! Gruss elementaar -
Spiel auf Dreier-Figuren mit Plus-Progression
topic antwortete auf elementaar's mamarketing in: Einfache Chancen
Hallo @Hans Dampf (von), Zur Illustration der Aussage von @Ropro noch drei Diagramme mit Trefferanzahl genau im Erwartungswert. Als Abschluss doch noch eine Tabelle. Hier wird in 30 ausgewählten Stichproben dargestellt, wie 111 Coups verlaufen können, wenn am Ende 18 Treffer (=Erwartungswert) erzielt wurden. Um auf 30 Stichproben mit dem Kriterium "18 Treffer" zu kommen, mussten in diesem Fall 242 Versuche gemacht werden (Anteil "18 Treffer" = 12,40%). Fröhliches Studieren! Gruss elementaar -
Spiel auf Dreier-Figuren mit Plus-Progression
topic antwortete auf elementaar's mamarketing in: Einfache Chancen
Hallo @Feuerstein, Das geht mir auch so. Das Tabellenlesen stellt höhere Anforderungen an das Vorstellungsvermögen und die in Tabellen enthaltenen Befunde muss man sich eher erarbeiten als intuitiv erfassen. Aber selbst die oben durchgeführte Miniuntersuchung mit jeweils 30 Stichproben, würde so 30 Diagramme untereinander erfordern - das will ich dann doch niemandem zumuten, obwohl der Erkenntniswert, meiner Meinung nach, damit deutlich höher wäre. Gruss elementaar -
Spiel auf Dreier-Figuren mit Plus-Progression
topic antwortete auf elementaar's mamarketing in: Einfache Chancen
Hallo @Hans Dampf (von), vielen Dank für Deine entspannte Antwort. Sie hat mir Freude gemacht. Als Anschauungsbeispiele, wie sich die Saldoverlaufskurven mit der Progression entwickeln können, einige Diagramme (ob wir von Tabellen zu Diagrammen uns steigern oder regredieren, soll jetzt nicht die Frage sein). Beispiel für Trefferanzahl im Erwartungswert: Beispiel für Trefferanzahl deutlich über Erwartungswert: Beispiel für Trefferanzahl deutlich unter Erwartungswert: Gruss elementaar -
Spiel auf Dreier-Figuren mit Plus-Progression
topic antwortete auf elementaar's mamarketing in: Einfache Chancen
Hallo @Hans Dampf (von), weiterhin nach Deinen Vorgaben, ähnliche Tabellen zum Spiel auf TP (Satz auf TP1) und Plein (Satz auf EZ1) Zunächst Spiel auf TP1: Zur Vergleichbarkeit wieder 30 Stichproben, diesmal jeweils mit einer Spielstrecke von 222 Coups für wieder 18 Rotationen der Chancengröße. Aus mehreren dieser 30er-Päckchen habe ich eines mit einem ähnlichen, leichten Trefferüberschuß ausgewählt (Soll= 540; Ist: TS= 555; TP= 553). Vielleicht interessant, je nach dem, wie es mit der Progression läuft, das Endergebnis, welches noch ein wenig schlechter ist, als Gleichsatzspiel. Sodann Spiel auf EZ1: Wieder 30 Stichproben, diesmal jeweils mit einer Spielstrecke von 666 (puh, was für eine Zahl!) Coups für 18 Rotationen der Chancengröße. Aus mehreren dieser 30er-Päckchen habe ich eines mit einem ähnlichen, leichten Trefferüberschuß ausgewählt (Soll= 540; Ist: TS= 555; TP= 553; EZ= 555). Es könnte als "unfreundlicher Akt" erscheinen, ausgerechnet einen bekennenden Tabellenallergiker mit eben diesen zuzuknallen, ich weiß aber leider keinen anderen Weg, so viele Daten in (noch) übersichtlicher Form zu liefern. Über andere, ebenso zielführende Präsentationsformen ließe sich allerdings diskutieren, falls Du diesbezüglich Vorschläge hättest. Gruss und schönen Sonntag! elementaar -
Spiel auf Dreier-Figuren mit Plus-Progression
topic antwortete auf elementaar's mamarketing in: Einfache Chancen
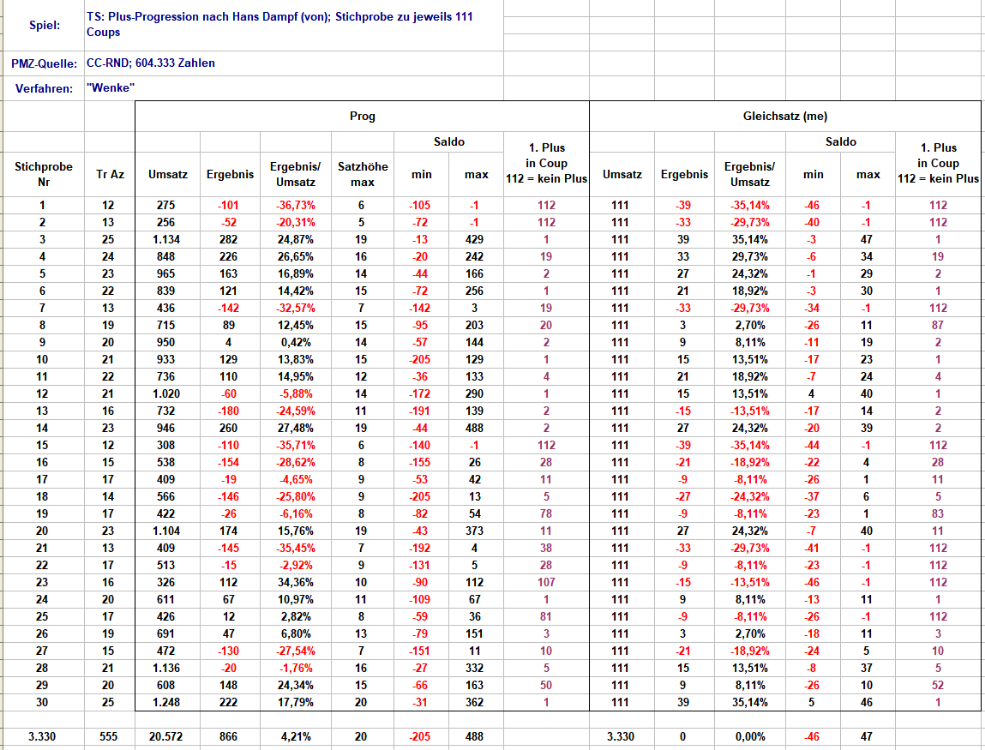
Hallo @Hans Dampf (von), Hier eine kleine Tabelle zum Spiel nach Deinen Vorgaben. Es wurde in jedem Coup TS 1 gespielt. Ich habe 30 Stichproben gezogen, in denen jeweils eine Spielstrecke von 111 Coups betrachtet wurde. Diese 111 Coups entsprechen 18 Pleinrotationen und sind auch im Landcasino an einem Tag noch spielbar. Natürlich sind diese 30 Stichproben nicht viel, aber bei mehr würde die Darstellung der Einzelergebnisse zur Tapete. "Tr Az" bedeutet: Anzahl der Treffer auf 111 Coups. Ansonsten sollten die Tabellenköpfe selbsterklärend sein, sonst bitte nachfragen. In den beiden umrahmten Kästen befinden sich die Resultate einmal Deiner Progression und, rechts daneben, was ein Gleichsatzspiel produziert hätte. Die Summe der 30 Stichproben ergibt eine leicht erhöhte Trefferdichte zum Erwartungswert (Soll: 540 zu Ist: 555) in dieser Betrachtungsstrecke; die Einzelergebnisse spiegeln also ein geschöntes Bild der erwarteten Wirklichkeit. Gruss elementaar -
Spiel auf Dreier-Figuren mit Plus-Progression
topic antwortete auf elementaar's mamarketing in: Einfache Chancen